Jayalk97
- 45
- 5
Please post this type of questions in HW section using the template.
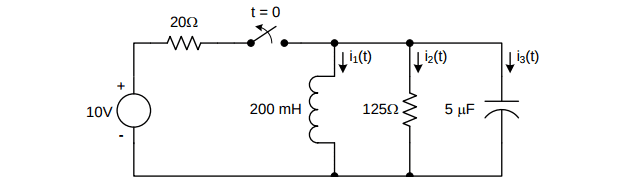
Hey guys, so I'm having trouble with this circuit analysis question. I need to find voltage across the capacitor as a function of time. I nearly finished analyzing but I'm having trouble solving for the initial value constants in the voltage equation. So first I used KCL to create the equation, then created a characteristic equation to find the type of response, which ended up being under-damped. I'm not trying to get any help with the acgtual numbers, but I end up with the equation v(t) = [A_1 cos(600t)+A_2 sin(600t)]e^(-800t). I'm fairly sure I'm correct so far, but how would I go about solving for A_1 and A_2? Thanks in advance!