PleaseAnswerOnegai
- 13
- 1
Summary:: I think we are still in the earlier parts of Physics and I am confused at how "values" work for a velocity-time graph. We are using the formulas to solve an area of a triangle and rectangle to find the total displacement. If a diagonal line begins from above and continue to go down, that denotes a negative velocity but in solving for the height of a triangle, will it also be negative?
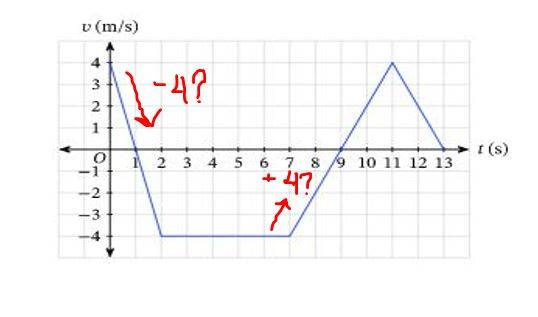
For the area of triangle, we use " 1/2(b)(h) ". For the first triangle will its height be a -4 in solving, as the line is going down therefore it is decelerating, or should I use a positive 4? How about the two other triangles in the trapezoid? How about the rectangle, will its height be -4?
We were asked to solve the displacement within the time frame of (0,9) so the triangle beyond that is not a concern for me at the moment.
For the area of triangle, we use " 1/2(b)(h) ". For the first triangle will its height be a -4 in solving, as the line is going down therefore it is decelerating, or should I use a positive 4? How about the two other triangles in the trapezoid? How about the rectangle, will its height be -4?
We were asked to solve the displacement within the time frame of (0,9) so the triangle beyond that is not a concern for me at the moment.