- #1
chucho11028
- 9
- 0
- Homework Statement
- calculate velocity using the graph
- Relevant Equations
- d=v*t
vf=vo+1/2*a*t
Hello
This is not a homework, this is my own experiment to understand how the motion works. Please, follow my question here below:
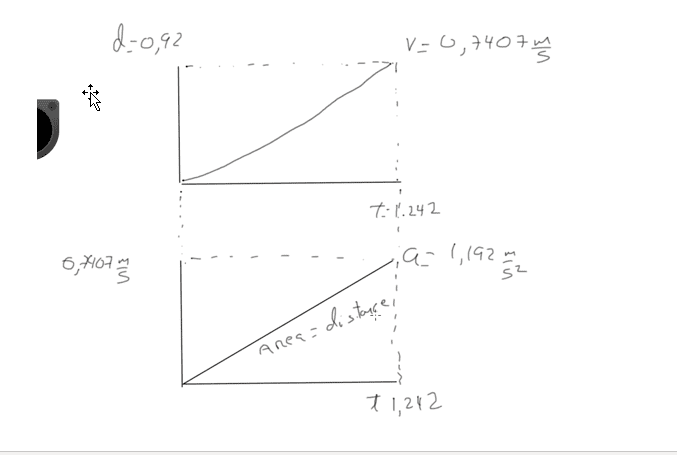
I have a hot wheels race with a slope with 10 degrees where I use a small car which departs from the top to the bottom. I have taken 5 times the time to get an average which is 1.242 seconds and the distance is 92 cent which 0.92 m.
Using the formula for distance d=v*t, I know my final velocity is 0.7407 m/s then, I have two graphs:
First graph, velocity and time, where I assume the velocity is increasing constantly and it will reflect a parabolic curve. I have attached the graph
Second graph, velocity and time, where I have a line with a slope which it should be the acceleration.So, my question is:
I know the area between velocity and time should be the distance, but this area is a triangle, so if I multiply time by velocity and divide by 2 it won’t give me .92 cm. I t will give a half. The only way to get the distance is using the rectangle but it would be wrong. Where is my mistake?
Regards,

This is not a homework, this is my own experiment to understand how the motion works. Please, follow my question here below:
I have a hot wheels race with a slope with 10 degrees where I use a small car which departs from the top to the bottom. I have taken 5 times the time to get an average which is 1.242 seconds and the distance is 92 cent which 0.92 m.
Using the formula for distance d=v*t, I know my final velocity is 0.7407 m/s then, I have two graphs:
First graph, velocity and time, where I assume the velocity is increasing constantly and it will reflect a parabolic curve. I have attached the graph
Second graph, velocity and time, where I have a line with a slope which it should be the acceleration.So, my question is:
I know the area between velocity and time should be the distance, but this area is a triangle, so if I multiply time by velocity and divide by 2 it won’t give me .92 cm. I t will give a half. The only way to get the distance is using the rectangle but it would be wrong. Where is my mistake?
Regards,
Attachments
Last edited by a moderator:

