Understanding AVL Tree Rotations: Solving the Case RL

[evinda]

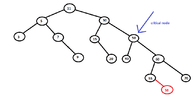
Hello! (Smile)We want to insert $58$ at the following AVL-tree and then we have to make rotations so that the tree is balanced. According to my notes, we are at the case [m]RL[/m] (The first edge leads to the right and the second to the left), where two rotations are required, one right around the next of the critical node and a left one, around the critical node.

View attachment 3879

But why are we at the case RL, although the first edge from the critical point to the new-inserted element is a left one and the second a right one? (Thinking)PS: The first node at the path from the node v (the new-inserted node) to the root, of which [m]balance=ReightHeight(v)-LeftHeight(v)[/m] was [m]-1[/m] or [m]1[/m](before the insertion) is called critical node.

 

[Future Bruno]

We are at the case RL because we are considering the path of edges from the node v (the new-inserted node) to the root. The first edge leading from the critical point to the new-inserted element is a left one and the second a right one, so this is the case RL.