SUMMARY
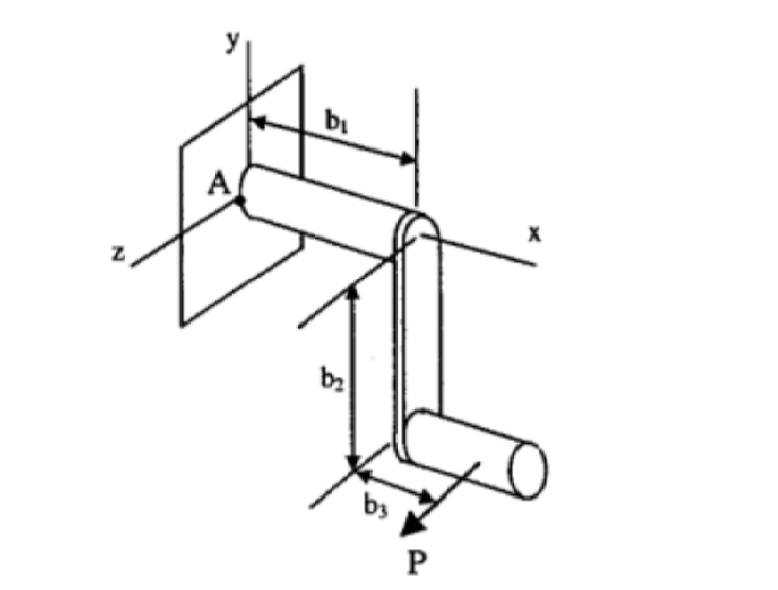
The correct formula for calculating the bending moment at point A in a crankshaft system is M = P * (b1 + b2), where P is the load applied. The discussion clarifies that the torque about point A is given by the vector equation, M = (b1 + b2 + b3) × P, but emphasizes that only the torque about the X-axis is relevant for analyzing the mechanism's effectiveness. The book answer is deemed incorrect, potentially due to a misquotation or misunderstanding of the problem statement. The dimensions provided are b1 = 80 mm, b2 = 120 mm, and b3 = 40 mm, with a load P of 1 kN.
PREREQUISITES
- Understanding of bending moment calculations in mechanical systems
- Familiarity with vector notation in physics
- Knowledge of shear and bending stress concepts
- Basic principles of torque and rotational mechanics
NEXT STEPS
- Study the principles of bending moment and shear stress in mechanical engineering
- Learn about the application of vector equations in torque calculations
- Research the effects of different loads on crankshaft performance
- Explore the design considerations for supporting sleeves in rotating shafts
USEFUL FOR
Mechanical engineers, students studying mechanics of materials, and professionals involved in the design and analysis of rotating machinery will benefit from this discussion.