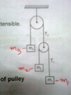
Understanding Different Accelerations in Constrained Pulley Motion

AI Thread Summary
The acceleration of masses m1 and m2 can differ due to the movement of the pulley they are attached to, which is influenced by mass m3. When one mass moves upward, its acceleration is augmented, while the downward-moving mass experiences a diminished acceleration. This difference arises from the dynamics of the pulley system, where the motion of the pulley affects the tension in the strings. Analyzing the system with free-body diagrams can clarify these relationships. Understanding these concepts is crucial for solving problems involving constrained pulley motion.
anigeo
Messages
83
Reaction score
0
could you please tell me how can the accelaration of masses m1 and m2 can be different.
i am in a great necessity.so please explain me how can the two strings of the two sides of the lower pulley have different accelarations?
 

Attachments

  • GB0750.jpg
    GB0750.jpg
    14.2 KB · Views: 530
Physics news on Phys.org
A good start: draw some free-body diagrams.
 
The lower masses have different accelerations due to the fact that the pulley they are attached to is itself moves due to the mass m3. So the mass moving upward will have an augmented acceleration while the mass moving downward will have a diminished acceleration. (Everything being viewed from an inertial frame like the constant surroundings.)
 

Thread '1:1 versus 2:1 Mechanical Advantage debate'

The rope is tied into the person (the load of 200 pounds) and the rope goes up from the person to a fixed pulley and back down to his hands. He hauls the rope to suspend himself in the air. What is the mechanical advantage of the system? The person will indeed only have to lift half of his body weight (roughly 100 pounds) because he now lessened the load by that same amount. This APPEARS to be a 2:1 because he can hold himself with half the force, but my question is: is that mechanical...
View full post »

Thread 'Newton's first law?'

Some physics textbook writer told me that Newton's first law applies only on bodies that feel no interactions at all. He said that if a body is on rest or moves in constant velocity, there is no external force acting on it. But I have heard another form of the law that says the net force acting on a body must be zero. This means there is interactions involved after all. So which one is correct?
View full post »
Thread 'Beam on an inclined plane'

Thread 'Beam on an inclined plane'

Hello! I have a question regarding a beam on an inclined plane. I was considering a beam resting on two supports attached to an inclined plane. I was almost sure that the lower support must be more loaded. My imagination about this problem is shown in the picture below. Here is how I wrote the condition of equilibrium forces: $$ \begin{cases} F_{g\parallel}=F_{t1}+F_{t2}, \\ F_{g\perp}=F_{r1}+F_{r2} \end{cases}. $$ On the other hand...
View full post »

Similar threads

I Translational force of a pulley
Replies
27
Views
2K
How Does Mass Affect the Direction of Rotational Motion in a Pulley System?
Replies
2
Views
1K
Does the Relation ##T_2 = T_1 e^{\mu \theta}## Hold for an Accelerating Capstan?
Replies
1
Views
1K
Why are these pulleys equivalent?
Replies
16
Views
1K
Pulleys with Strings Having Mass
Replies
4
Views
3K
1 pulley with mass, 1 mass on the cord, 1 external force, no gravity
Replies
16
Views
3K
Velocity of Pulley and String in Constrained Motion
Replies
1
Views
3K
Accelerating motion with a pulley
Replies
10
Views
2K
Olympiad dynamics problem with 3 masses and a pulley
Replies
17
Views
2K
A simple pulley two mass system
Replies
7
Views
3K

Hot Threads

Recent Insights

Back
Top