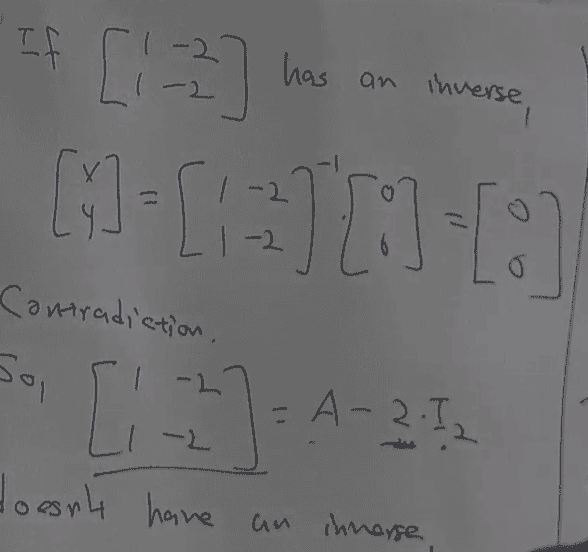The discussion centers on understanding the eigenvalues of a singular matrix, specifically the matrix A = [ -1, -2; 1, -4 ]. Participants clarify that the matrix does not possess an inverse due to its one-dimensional image in ℝ², which prevents it from mapping onto the entire space. The eigenvalues identified are -2 and -3, corresponding to eigenvectors x₁ and x₂ respectively, confirming the matrix's singularity and the validity of the eigenvalue equations.
PREREQUISITESStudents of linear algebra, mathematicians, and educators seeking a deeper understanding of eigenvalues, particularly in the context of singular matrices and their properties.
Me, too. I don't know what this means. ##A\cdot 0=0## no matter whether ##A## is invertible or not.ChiralSuperfields said:
The matrix doesn't have an inverse. If we want to prove this by contradiction then we assume it has an inverse. Say the matrix is ##A.## Then ##A## maps the entire space ##\mathbb{R}^2## onto itself: ##A\cdot v= w.## Now, if we set ##v=\begin{pmatrix}x\\ y\end{pmatrix}## then ##A\cdot v=\begin{pmatrix}-x+2y\\-x+2y\end{pmatrix}.## But this means that both coordinates of ##w## are the same and we have no chance to get any other vector with different coordinates. So the image of ##A## is one-dimensional, not two-dimensional, so it cannot be invertible.ChiralSuperfields said: