SUMMARY
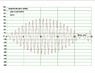
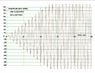
The discussion centers on the dynamics of a pendulum subjected to a periodic harmonic driving force, specifically when the driving frequency matches the natural frequency of the pendulum. It is established that if the driving force frequency is slightly less than the natural frequency, the pendulum will eventually oscillate in phase with the driving force, leading to resonance and increased amplitude. Conversely, if the driving frequency exceeds the natural frequency, the pendulum will oscillate 180 degrees out of phase, resulting in no net energy exchange. The analysis is supported by differential equations and simulations, revealing that the initial phase of the oscillator becomes irrelevant over time, particularly in a frictionless environment.
PREREQUISITES
- Understanding of harmonic oscillators and resonance phenomena
- Familiarity with differential equations and their solutions
- Knowledge of phase relationships in oscillatory systems
- Experience with simulations of physical systems, particularly in a frictionless context
NEXT STEPS
- Study the effects of damping on forced harmonic oscillators
- Explore the mathematical modeling of driven oscillators using differential equations
- Investigate the concept of beat frequency in oscillatory systems
- Learn about phase shifts in harmonic motion and their implications for energy transfer
USEFUL FOR
Physicists, engineers, and students studying dynamics, particularly those interested in oscillatory motion and resonance in mechanical systems.