Understanding gyro without angular mom

In summary, the speaker is seeking a Newtonian explanation for the motion of a gyroscope and is struggling to understand precession without invoking angular momentum and torque. They provide a diagram and mention thinking of the flywheel as a composite object to better understand the concept. Another speaker suggests using the ping pong ball on a string analogy to better understand the effect of precession on the gyroscope's rotation.
  • #1
h0dgey84bc
160
0
Hi,

I understand the motion of a gyroscope through considerations of torque and angular momentum, I have no issue with deriving it and imagining it by considering these things, but I somehow feel I still don't understand precession on an intuitive level. I was wondering if anyone could help me understand the motion of a gyroscope without invoking angular momentum/torque, just by soley considering Newton's laws.

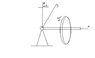
Just to avoid confusion, take the z axis as out of the screen, y-axis from bottom to top, x-axis from left to right and I'm considering a flywheel rotating along an axis in the x-direction. Its axial rod is sat on a pivot to the left, gravity is in the negative z direction. Hence torque is in the y-direction, and precession occurs about the z axis.
I've attempted a drawing, that I've attached.

Like I say, I'm happy with the ang mom/torque explanation, I am just looking for a Newtonian one.

Thanks
 

Attachments

  • precession.jpg
    precession.jpg
    6 KB · Views: 325
Physics news on Phys.org
  • #2
Don't be afraid of angular momentum. You really need it here.
Even Newton used it.
 
  • #3
clem said:
Don't be afraid of angular momentum. You really need it here.
Even Newton used it.

I'm not afraid of angular momentum, I fully understand the explanation of precession via angular momentum and torque, and no issues with it at all. However I have an itching to understand this via simple forces as well, ultimatley such a picture must be possible here. I think that thinking of the flywheel as a composite object, made up of smaller particles, some of which are moving up, some down, some left some right, etc, when the flywheel spins, is key to understanding why the flywheel precesses when spun, but falls otherwise. Can't quite fully picture it just yet though.
 
  • #4
I never understood gyroscopes (I still dont) until I read the ping pong ball on a string explanation. as the ball circles around each time it strikes a paddle and glances off at a very slight angle. the result is a downward force on the paddle. you can then easily imagine the effect on the ping pong balls rotation.
 

1. What is a gyro and how does it work?

A gyro, short for gyroscope, is a device that is used to measure or maintain orientation and angular velocity. It consists of a spinning wheel or disc that is mounted on a set of gimbals, allowing it to rotate freely in any direction. When the gyro is rotated or tilted, it maintains its original orientation due to the principle of angular momentum.

2. What is angular momentum and how does it relate to gyroscopes?

Angular momentum is a physical quantity that describes the amount of rotational motion an object possesses. It is a product of the object's moment of inertia and its angular velocity. In gyroscopes, angular momentum is important because it allows the gyro to remain stable and maintain its orientation even when subjected to external forces.

3. How is gyroscopic stabilization used in different applications?

Gyroscopic stabilization is used in a variety of applications, including navigation systems, aircraft and spacecraft control, and even toys like the spinning top. It is also commonly used in mechanical gyroscopes to measure rotation and provide stability for devices like cameras and compasses.

4. Can a gyro lose its angular momentum?

Yes, a gyro can lose its angular momentum due to external forces acting on it or friction within the device. This can cause the gyro to eventually slow down and stop spinning, leading to a loss of stability. However, gyroscopes are designed to minimize these effects and can maintain their angular momentum for a significant amount of time.

5. How does understanding gyro without angular momentum help in designing better gyroscopes?

Understanding gyro without angular momentum is crucial in designing more efficient and accurate gyroscopes. By understanding the principles of angular momentum and its relationship with gyroscopes, scientists and engineers can develop better designs that minimize external forces and friction, resulting in more reliable and precise gyroscopes for various applications.

Similar threads

I Torque required to prevent precession
    • Classical Physics
Replies
2
Views
868
I What Determines the Order of Rotations for a Gyro?
    • Classical Physics
Replies
2
Views
959
I What does weight actually do in gyroscopic precession?
    • Classical Physics
Replies
7
Views
1K
I Gyroscopic precession of a spin-stabilized bullet
    • Classical Physics
Replies
10
Views
1K
I Does Larmor precession change the force exerted on a magnetic dipole?
    • Classical Physics
Replies
1
Views
642
A Degrees of freedom of thin rods
    • Classical Physics
Replies
7
Views
1K
What happens to energy in a gyro vs. flywheel problem?
    • Classical Physics
Replies
9
Views
4K
I PIGA: Pendulous Integrating Gyroscopic Accelerometer
    • Mechanics
Replies
0
Views
514
I A scientific analysis of stopping the spin of Discovery One spaceship
    • Classical Physics
Replies
3
Views
917
B Clashing approximations for this precession problem
    • Classical Physics
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top