Understanding Impedance: How to Find Poles and Zeros of a Network

[roam]

Homework Statement

I have some trouble understanding the worked examples below:

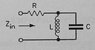
Considering the input impedance of the network below:

$z_{in} = R+ \frac{sL/sC}{sL+(1/sC)}$

$z_{in} = R \left[ \frac{s^2+s/(RC)+1/(LC)}{s^2+1/(LC)} \right]$

Where $s=j\omega$.

How did they get from the first expression to the second expression?

The Attempt at a Solution

Clearly looking into the network R is in series with the parallel combination of L and C, so we have $R + L \parallel C$ which is the first expression:

$z_{in} = R+ \frac{sL/sC}{sL+(1/sC)}$

We can further write this as:

$z_{in} = R+ \frac{sRL + (R/sC)+(sL/sC)}{sL+(1/sC)}$

I'm really confused. Where does the second expression given above come from?

Any help is greatly appreciated.

P.S. This is part of a problem about finding poles and zeros of the network. The quadratics in the numerator and denominator of the 2nd expression can be factorized to give the poles and zeros.

 

[rude man]

Just algebra!
1. cross-multiply
2. factor out R, this means putting a 1/R coefficient in one term.
3. divide numerator & denominator by L.

 

[The Electrician]

We can further write this as:

$z_{in} = R+ \frac{sRL + (R/sC)+(sL/sC)}{sL+(1/sC)}$

The above expression is incorrect; the initial R+ shouldn't be there. The expression should be:
$z_{in} = \frac{sRL + (R/sC)+(sL/sC)}{sL+(1/sC)}$

 

[rude man]

Your second equation has a typo (the first R). The thumbnail is correct.

 

[roam]

Thank you very much, I got the right answer now! :)