- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
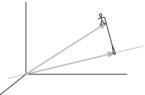
Let $\phi_1:\mathbb{R}^3\rightarrow \mathbb{R}^3$, $v\mapsto \begin{pmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{pmatrix}\cdot v$, $\phi_2:\mathbb{R}^3\rightarrow \mathbb{R}^3$, $v\mapsto \frac{1}{3}\begin{pmatrix}2 & - 1& - 1\\ - 1& 2 & -1\\ - 1&-1 & 2\end{pmatrix}\cdot v$ which describes the shadow of the sun on a plane.
Give the direction of the sun by giving a vector. How do we find this vector? (Wondering)
To give the equation of the plane do we have to find the image of the map? (Wondering)
How can we explain why at a projection $\psi$ it holds that $\psi\circ\psi=\psi$ and $\text{im} \psi=\text{fix} \psi$? (Wondering)
Let $\phi_1:\mathbb{R}^3\rightarrow \mathbb{R}^3$, $v\mapsto \begin{pmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{pmatrix}\cdot v$, $\phi_2:\mathbb{R}^3\rightarrow \mathbb{R}^3$, $v\mapsto \frac{1}{3}\begin{pmatrix}2 & - 1& - 1\\ - 1& 2 & -1\\ - 1&-1 & 2\end{pmatrix}\cdot v$ which describes the shadow of the sun on a plane.
Give the direction of the sun by giving a vector. How do we find this vector? (Wondering)
To give the equation of the plane do we have to find the image of the map? (Wondering)
How can we explain why at a projection $\psi$ it holds that $\psi\circ\psi=\psi$ and $\text{im} \psi=\text{fix} \psi$? (Wondering)