jdou86
- 34
- 1
- TL;DR Summary
- Hi all I would like to understand this concept please help.
Summary: Hi all I would like to understand this concept please help.
I understand the montonic convergence theorem this is from a probability theory book and I am confused on understanding it. Please help me understand it.
Thank you very much,Jon.
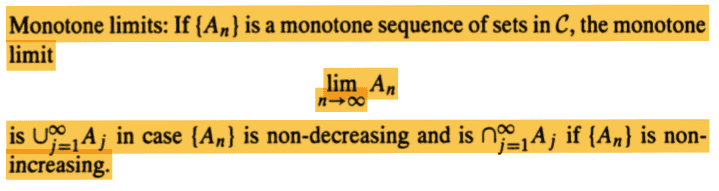
I understand the montonic convergence theorem this is from a probability theory book and I am confused on understanding it. Please help me understand it.
Thank you very much,Jon.