namster
- 2
- 0
Summary:: Conversion from quaternion to DCM
Hi All ,
our teacher asked us to try to understand the openshoe Matlab library , i stagnate on function that convert the quaternion to DCM i have found many example on website but the description of matrix are diffrente that the one is used on openshoe but it give the same result , so i wan't to know which of this matrix is correcte ?
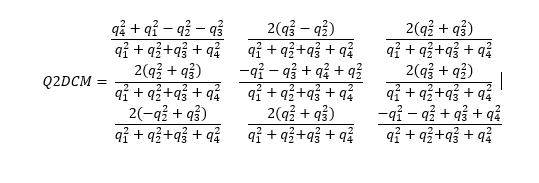
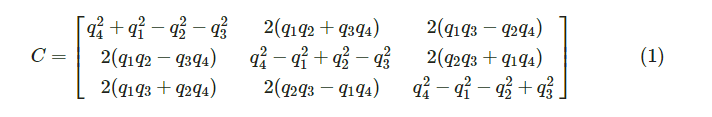
Hi All ,
our teacher asked us to try to understand the openshoe Matlab library , i stagnate on function that convert the quaternion to DCM i have found many example on website but the description of matrix are diffrente that the one is used on openshoe but it give the same result , so i wan't to know which of this matrix is correcte ?