Understanding ray diagrams for concave lenses

[Kyle91]

Hey guys,

So some friends and I are studying for a test and we came across this question. I've absolutely no idea what the answer is simply because every website I've found only shows parallel rays and a ray going through the centre of the lens. It's incredibly aggravating.

Anyway here's the question -

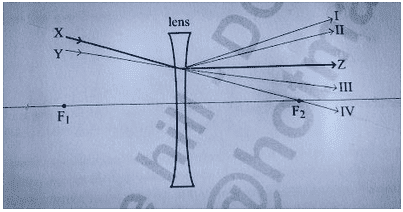
Ray X became Ray Z when passing through the lens. Which does Ray Y become?

As I said, every website/textbook/youtube video skips this info so I don't have a guess. Can you please not make me work for the answer. I'll understand it if you just tell me. I don't want to hate studying - I just want to know.

Thank you

 

[jtbell]

Sorry, our philosophy here is not to simply give answers to questions like this.

You might start by extrapolating ray Y to the point where it would intersect the axis if the lens were not there. That tells you the location of the (virtual) object associated with that ray.

 

[Vargo]

I don't know much about the physics here, but I read about this in a book on symplectic methods in physics. Apparently, if you take any plane perpendicular to the F1F2 axis, then you can characterize a ray passing through that plane with two numbers:

q = height of intersection.
p = (slope of the ray) *(index of refraction)

The values of q and p depend on the plane you choose. But if you choose two different planes, then the corresponding q and p values are related by a matrix whose determinant equals 1.

q' = aq + bp
p' = cq + dp,

ad - bc = 1.

This is called linear optics and is an approximation of proper geometric optics.

So anyway, if you take the two planes just on either side of a thin lens, then (because the lens is very thin), the height remains unchanged from one side to the other. So a=1, b=0.
And if the incoming height is 0 (i.e. the ray intersects the lens along the central axis), then the slopes are unchanged because the lens is flat there. So d=1. (But you could also deduce this from ad-bc=1)

Anyway, the coefficient c is related to the concavity of the interface and the difference in index of refraction of the lens and the index of refraction of the ambient space (air?).

Presumably the index of refraction to the left of the lens is equal to the index to the right, so p and p' are proportional to the ingoing and outgoing slopes with the same proportionality constant. You can take this further to find the answer to your question.

Anyway, I thought I would put this down because your question reminded me of this stuff I read about a long time ago. And because I am guessing the linear approach is different from the one in your class. It has the benefit of being a powerful method that is easy to employ. However, it is limited to things like thin lenses in which a linearization of the true optics problem is valid. Also, since it is fairly formal, it does not necessarily add to your understanding of the physics.

 

[deep838]

for a concave lens, the incident ray diverges outward from its actual path... here the ray X becomes parallel after refraction... and ray Y is coming from below X... so that narrows down the possibilities of the final path of Y.