almarpa
- 94
- 3
Hello all.
I have a doubt about the derivation of energy in dielectrics formula (Griffiths pages 191 - 192).
In a certain step of the formula derivation, we encounter the following operation:
(view formula below).
I do not undertand that operation.
Can someone help me?
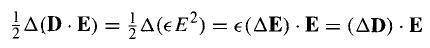
I have a doubt about the derivation of energy in dielectrics formula (Griffiths pages 191 - 192).
In a certain step of the formula derivation, we encounter the following operation:
(view formula below).
I do not undertand that operation.
Can someone help me?
Last edited by a moderator: