sacred
- 4
- 0
This could be seen as a rather "basic" math question, but it is a topic of curiosity for me. I'm currently a senior in high school, taking a pre-ap pre-cal/trig/AP-Calculus double blocked class. I'm absolutely fascinated by mathematics, and something of keen interest to me is the derivation of the quadratic formula. Not only do I wonder who originally derived it and how they did it, but I want to completely understand it. (Again, I can see how some people would laugh at this, because it's not that hard to understand) However, there is one part that completely blows my mind:
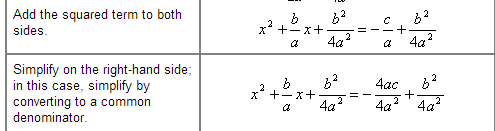
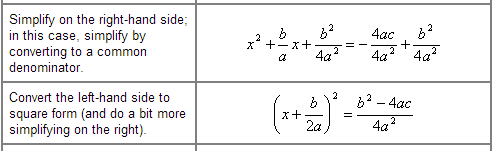
How exactly does this simplify? I've sat here staring at it, attempting to conceptualize it so I can continue... but I just can't. I don't understand it. Would someone care to explain?
Thank you,
sacred
edit: reading some other threads on this board... I feel like a complete idiot... bare with me
edit2: I can understand the right side, but not the left.
How exactly does this simplify? I've sat here staring at it, attempting to conceptualize it so I can continue... but I just can't. I don't understand it. Would someone care to explain?
Thank you,
sacred
edit: reading some other threads on this board... I feel like a complete idiot... bare with me
edit2: I can understand the right side, but not the left.
Attachments
Last edited: