Master1022
- 590
- 116
- TL;DR
- If we are given a set of stress state equations and we want to 'rotate' them, which direction shall I use?
Hi,
The context for my question is: A thin plate, which lies in the x-y plane, contains a small hole of radius a. Consider a polar co-ordinate system r, with its origin at the centre of the hole and defined as the angle that a radial line makes with the x-axis. A uniform uniaxial tensile stress \sigma^{app}_x is applied to the plate in the x-direction. The stress state in the plate is:
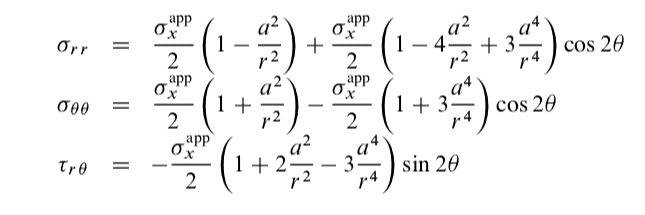
Determine the state of stress in a plate that is subjected to a uniform uniaxial tensile stress \sigma^{app}_y which is aligned with the y-direction.
My Method: I defined some new angle \phi = \theta + 90 (CCW) (with the main point being that I chose to define it with a +). Following on, I got that: \sin(2(\theta + 90)) = -\sin(\theta) and that \cos(2(\theta + 90)) = -\cos(\theta). Then we just substitute those into the three equations and change \sigma^{app}_x to \sigma^{app}_y to get the answer. The answers come out the same in this instance regardless of the direction of definition of the new angle. However, in later parts of the question, we basically follow the same method for rotating the state by 45 degrees, and the direction makes a difference there (some signs are different).
My question: Why has the solution chosen to define the 'new' \theta_{new} = \theta_{old} - 90 (CW)?
(Note: I only posted the earlier question as the same exact concept applies to the later one, but there are more parts between now and then which would just unnecessarily add to the reading time)
The context for my question is: A thin plate, which lies in the x-y plane, contains a small hole of radius a. Consider a polar co-ordinate system r, with its origin at the centre of the hole and defined as the angle that a radial line makes with the x-axis. A uniform uniaxial tensile stress \sigma^{app}_x is applied to the plate in the x-direction. The stress state in the plate is:
Determine the state of stress in a plate that is subjected to a uniform uniaxial tensile stress \sigma^{app}_y which is aligned with the y-direction.
My Method: I defined some new angle \phi = \theta + 90 (CCW) (with the main point being that I chose to define it with a +). Following on, I got that: \sin(2(\theta + 90)) = -\sin(\theta) and that \cos(2(\theta + 90)) = -\cos(\theta). Then we just substitute those into the three equations and change \sigma^{app}_x to \sigma^{app}_y to get the answer. The answers come out the same in this instance regardless of the direction of definition of the new angle. However, in later parts of the question, we basically follow the same method for rotating the state by 45 degrees, and the direction makes a difference there (some signs are different).
My question: Why has the solution chosen to define the 'new' \theta_{new} = \theta_{old} - 90 (CW)?
(Note: I only posted the earlier question as the same exact concept applies to the later one, but there are more parts between now and then which would just unnecessarily add to the reading time)
Last edited: