I Understanding the Form of the Y(2,0) Spherical Harmonic

[Archeon]

I am basically just rewriting a question that was posted on other forums.
While watching videos of a MIT lecture on the eigenstates of angular momentum (video: '16. Eigenstates of the Angular Momentum II' by MIT OpenCourseWare) the professor visualized different spherical harmonics for low values of the quantum number l. He showed that for Y(l = 1, m = 0) the function has the following form:

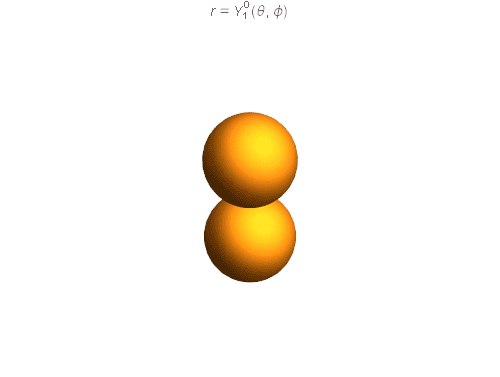
explaining that since m=0 there is no angular momentum L_z and the probability of finding it in the x-y plane is practically zero.
He then went on to show the Y(l=2, m=0) state, as seen below:

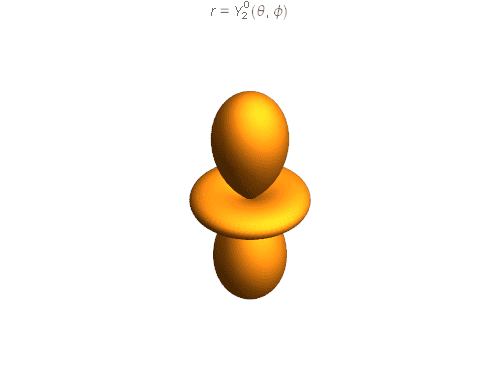
This strikes me as odd, however, as the disk around the z-axis would imply to me that there is a good probability that the particle is spinning along the z-axis and as a result carries some angular momentum L_z > 0. How, if at all possible, can this phenomenon be explained intuitively?

Thanks in advance

 

[PeroK]

This strikes me as odd, however, as the disk around the z-axis would imply to me that there is a good probability that the particle is spinning along the z-axis and as a result carries some angular momentum L_z > 0. How, if at all possible, can this phenomenon be explained intuitively?

Thanks in advance

The disk around the z-axis implies that the particle might be found there. It doesn't mean that the particle is following any sort of orbit that has that shape.

More generally, you can't really say the particle has an orbit at all (not in the classical sense).

 

[DrClaude]

This strikes me as odd, however, as the disk around the z-axis would imply to me that there is a good probability that the particle is spinning along the z-axis and as a result carries some angular momentum L_z > 0. How, if at all possible, can this phenomenon be explained intuitively?

You have to let go of classical pictures. The particle is not moving inside the orbital. They represent stationary states.

 

[Archeon]

I see. Thanks for the clear answers.