JD_PM
- 1,125
- 156
Homework Statement:: I am studying how to compute the meson-decay amplitude worked out in Tong's notes (pages 55 and 56; I attached the PDF).
Relevant Equations:: $$<f|S|i>=-ig<f| \int d^4 x \psi^{\dagger} (x) \psi (x) \phi (x) |i>$$
The initial and final states are given by
$$|i > = \sqrt{2 E_{\vec p}} a_{\vec p}^{\dagger} |0>$$
$$|f > = \sqrt{4 E_{\vec q_1}E_{\vec q_2}} b_{\vec q_1}^{\dagger}c_{\vec q_2}^{\dagger} |0>$$
Using Dyson formula's expansion we get that
$$<f|S|i>=-ig<f| \int d^4 x \psi^{\dagger} (x) \psi (x) \phi (x) |i>$$
We first expand out ##\phi \sim a + a^{\dagger}## using the following formula
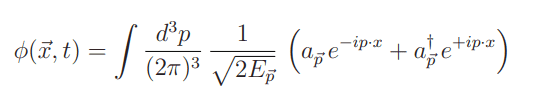
Doing so we get
$$<f|S|i>=-ig<f| \int d^4 x \psi^{\dagger} (x) \psi (x) \int \frac{d^3 k \sqrt{2E_{\vec p}}}{(2 \pi)^3 \sqrt{2E_{\vec k}}} a_{\vec k} a_{\vec p}^{\dagger} e^{-ikx} |0> = -ig<f|\int d^4 x \psi^{\dagger} (x) \psi (x) e^{-ipx} |0>$$
I do not understand why the ##a_{\vec k}e^{ipx}## term vanishes.
Tong justifies it as follows: when ##a^{\dagger}## hits |i> we get a two meson state, which has 'zero overlap' with ##<f|## and 'and there’s nothing in the ##\psi## and ##\psi^{\dagger}## operators that lie between them to change this fact'.
What does he mean with 'zero overlap' with ##<f|##?
He uses the same argument to justify the final solution:
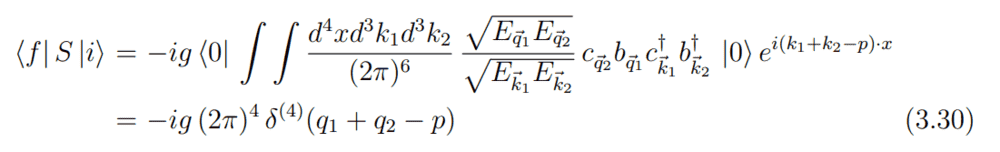
With this thread I am aimed at understanding and getting the provided solution.
Thank you.
PS: The amplitude can be computed by formula (3.26), The unitary matrix is given by formula (3.23), where the ##H_{int}## is given by (3.25)
Relevant Equations:: $$<f|S|i>=-ig<f| \int d^4 x \psi^{\dagger} (x) \psi (x) \phi (x) |i>$$
The initial and final states are given by
$$|i > = \sqrt{2 E_{\vec p}} a_{\vec p}^{\dagger} |0>$$
$$|f > = \sqrt{4 E_{\vec q_1}E_{\vec q_2}} b_{\vec q_1}^{\dagger}c_{\vec q_2}^{\dagger} |0>$$
Using Dyson formula's expansion we get that
$$<f|S|i>=-ig<f| \int d^4 x \psi^{\dagger} (x) \psi (x) \phi (x) |i>$$
We first expand out ##\phi \sim a + a^{\dagger}## using the following formula
Doing so we get
$$<f|S|i>=-ig<f| \int d^4 x \psi^{\dagger} (x) \psi (x) \int \frac{d^3 k \sqrt{2E_{\vec p}}}{(2 \pi)^3 \sqrt{2E_{\vec k}}} a_{\vec k} a_{\vec p}^{\dagger} e^{-ikx} |0> = -ig<f|\int d^4 x \psi^{\dagger} (x) \psi (x) e^{-ipx} |0>$$
I do not understand why the ##a_{\vec k}e^{ipx}## term vanishes.
Tong justifies it as follows: when ##a^{\dagger}## hits |i> we get a two meson state, which has 'zero overlap' with ##<f|## and 'and there’s nothing in the ##\psi## and ##\psi^{\dagger}## operators that lie between them to change this fact'.
What does he mean with 'zero overlap' with ##<f|##?
He uses the same argument to justify the final solution:
With this thread I am aimed at understanding and getting the provided solution.
Thank you.
PS: The amplitude can be computed by formula (3.26), The unitary matrix is given by formula (3.23), where the ##H_{int}## is given by (3.25)