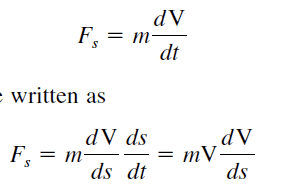Understanding Thermodynamics: Demystifying the Chain Rule for Integration

[th3plan]

I am reading a thermodynamics book. I am confused on how they say use the chain rule Here. it makes no sense to me how they go from dV/dt to (dV/ds)(ds/dt) . I know how the chain rule works ,just don't know where they got these values

 

[Cyosis]

Well they use the chain rule in the normal way here. If V is a function of s and s is a function of t, V(s(t)), then the chain rule tells you that (V \circ s)'(t)=V'(s(t))s'(t). Is that more familiar? This is Identical to \frac{dV}{ds}\frac{ds}{dt}. To display this a bit more clearly let's start with the function V(s(t)). We then use the chain rule by substituting u=s(t). So (V \circ s)'(t)=V'(u)u'=\frac{d V}{d u} \frac{d u}{d t}=\frac{d V}{d s} \frac{d s}{d t}.