Unexpected Zeta and Overshoot relation

[Wxfsa]

I have a designed feedback control system trying to minimize the overshoot and the setting time. The zeta I (think) ended up with is 0.94. According to this formula:

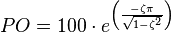
I am supposed to have a very small overshoot. However the step response of the system looks like this:

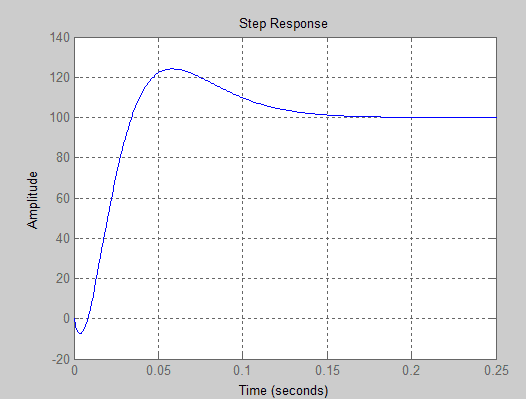
The poles are:
0.0000 + 0.0000i (0 is also a zero, so do they cancel?)
-2.0000 + 0.0000i
-0.5313 + 0.1740i
-0.5313 - 0.1740i
-0.5600 + 0.0000i
-0.0600 + 0.0000i

Does that formula apply only for second order system? Or must I have miscalculated something?

 

[rude man]

Does that formula apply only for second order system? Or must I have miscalculated something?

Yes, the pole & zero at the origin cancel.
Leaving you with a whopping 5th-order system. I wouldn't know any other way than to compute the actual response to a step input, eschewing any and all a priori formulas.

 

[Wxfsa]

Great, thanks.

 

[LvW]

Does that formula apply only for second order system? Or must I have miscalculated something?

Your 5th order system has only one dominant complex pole pair with a pole-Q of app. Qp=0.52. The remaining poles are negative-real.
Hence, I agree with you that we can expect a rather small overshoot only (assuming that the mentioned poles apply to closed-loop conditions).