Uniform Circular Motion and Centripetal Acceleration (non-intuitive)

[babaliaris]

I'm in the chapter of Uniform Circular Motion and I have a hard time understating centipetal acceleration. Until now I knew that acceleration describes "how fast velocity changes in magnitude" except projectile motion because when it reaches maximum height then g is going to change the direction on the Vy and make it move downwards but now in this kind of motion, acceleration describes only "how fast the direction of the velocity changes" and not the magnitude. Ok I understand that but what I really don't understand is when I'm in a car and take a turn I feel pushed in the opposite direction of the circles center. But acceleration is pointing at the center of the circle

 

[vanhees71]

Any change of the velocity (a vector!) means that there's non-zero acceleration, because by definition
$$\vec{a}(t)=\dot{\vec{v}}(t)=\ddot{\vec{x}}(t).$$
For the uniform motion on a circle (for convenience I put it in the $xy$=plane of the coordinate system) you have
$$\vec{x}(t)=r [\vec{e}_x \cos (\omega t) + \vec{e}_y \sin(\omega t)].$$
Now you can easily evaluate velocity and acceleration.

Then, using Newton's 2nd law you immediately get which force you have to apply to the particle to make it move in the described way along a circle.

 

[Ibix]

Until now I knew that acceleration describes "how fast velocity changes in magnitude"

No - acceleration is how fast velocity vector is changing (or, more precisely, the rate of change of the velocity vector). The magnitude only changes sometimes; the direction only changes sometimes. The vector always changes. I remember feeling weird about that too, but it must be that way. There's a force acting on a mass (e.g. a string pulling on a stone being swung around in a circle), and $F=ma$ tells you there must be an acceleration.

Ok I understand that but what I really don't understand is when I'm in a car and take a turn I feel pushed in the opposite direction of the circles center.

There are two ways of looking at this, and you are mixing them up.

The first way to look at a car going round a corner is from outside it. I'm standing on a bridge above the road, looking down on your car as you start to corner. What I see is that the car is cornering, but your body is trying to carry on in a straight line (Newton's First Law). But if you carry on in a straight line, the car door curves into you and presses you into a curve. That's the centripetal force, and it's my explanation for why you turn.

The second way to look at it is from inside the car. From this perspective, the world is turning and the car isn't moving. But you still need an explanation of why the door is pressing into you - mine doesn't make sense because the door doesn't turn in this perspective. Your explanation is the centrifugal force (sometimes called a fictitious force, or an inertial force) that just comes out of nowhere and presses you to the door.

The book is using the first perspective. It's mathematically a lot simpler to handle, but it's a bit counter-intuitive since we're seldom doing detailed analysis of the kinematics of a car passing underneath a bridge. The second explanation is the natural one for us since we're used to traveling in cars, but it involves more complex maths to explain what inertial forces are so physics textbooks tend to avoid it until further on in your education. I think I was taught it in my second year at university (although I don't think I grasped the significance until much later...)

 

[vanhees71]

The problem is that many books do not use the really simple mass, as I suggested to use in #2. Some textbook make very simple things very complicated by a misguided attempt to "avoid math". It should be very clear that math is helping to make things much simpler and cannot be avoided anyway. So one should introduce the appropriate math right away when it's useful for a given problem, rather than avoiding it. For mechanics you need vector algebra, derivatives and integrals as well as ordinary differential equations.

 

[Delta2]

That's true , you feel LIKE there is a force that is pushing you to the opposite direction of the centripetal acceleration.

But what you actually feel, is a force from the car's seat mainly, that is pushing you towards centripetal acceleration (so the force on your body from the car's seat is on the same direction as centripetal acceleration), and due to Newton's 3rd Law, your body is pushing the car's seat with an opposite force, that is your body is pushing the car's seat in a direction opposite to centripetal acceleration. That push from your body to the car's seat is what your wrongly understand as "being pushed in direction opposite of the centripetal acceleration".

 

[A.T.]

I'm in a car and take a turn I feel pushed in the opposite direction of the circles center. But acceleration is pointing at the center of the circle

When the car accelerates forward, you end up in the back of the car, if you are not fixed an thus fail to accelerate with the car. The same applies to accelerating left or right in a turn.

 

[babaliaris]

I'm a little confused... Well I still haven't reached the chapter about forces and Newton's laws. Now I'm in the relative motion chapter and next is the forces and motion chapter and Newton's first law. Do you thing I will have a better understating after that chapter?

 

[babaliaris]

When the car accelerates forward, you end up in the back of the car, if you are not fixed an thus fail to accelerate with the car. The same applies to accelerating left or right in a turn.

Best reply! Now I see! Well I can't wait to reach the chapter of forces and Newton's laws to get a deeper understanding!

 

[Delta2]

I'm a little confused... Well I still haven't reached the chapter about forces and Newton's laws. Now I'm in the relative motion chapter and next is the forces and motion chapter and Newton's first law. Do you thing I will have a better understating after that chapter?

Yes, in my opinion you absolutely need a good understanding of Newton's 2nd and 3rd law to fully understand what's going on.

 

[babaliaris]

Yes, in my opinion you absolutely need a good understanding of Newton's 2nd and 3rd law to fully understand what's going on.

Thanks for the advice!

 

[babaliaris]

That's true , you feel LIKE there is a force that is pushing you to the opposite direction of the centripetal acceleration.

But what you actually feel, is a force from the car's seat mainly, that is pushing you towards centripetal acceleration (so the force on your body from the car's seat is on the same direction as centripetal acceleration), and due to Newton's 3rd Law, your body is pushing the car's seat with an opposite force, that is your body is pushing the car's seat in a direction opposite to centripetal acceleration. That push from your body to the car's seat is what your wrongly understand as "being pushed in direction opposite of the centripetal acceleration".

Your answer make's the most sense now (i finished reading about uniform circular motion), but still i can't understand a few things. It's weird, i reached so far learned about motions, forces, Newton's laws and now I've stuck... When a particle move's in a uniform circular motion there is a Centripetal force towards the center.

Question 1:
So if we assume there is no gravity and no other forces applied on the particle, why the particle is not moving towards the center of the circle? So if I name r the axis where the Centripetal force is lying , according to Newton's second law:

∑ƒr = m⋅a ⇔ -ƒc = m ⋅ ( -v^2 / R ) ⇔ fc = m ⋅ ( v^2 / R ) but still i can't understand why the parcicle is moving in a circle and not towords the center. If you can use maths to explain use them.

Question 2:
Let's say i have a rope tied in a particle and I'm spinning it (around a y axis) with my hand. Then the particle is entering a uniform circular motion but also it does not fall to the ground and according to Newton there must be another force with the same magnitude as Fg (weight) in the opposite direction so the particle won't move at all on the y axis. Also if i speed faster and increase the constant speed of the uniform circular motion, the rope will break. Consider the following sketch:

I have a really hard time understanding the cause of these forces. It must F = -Fg so the particle won't fall to the ground or actually won't move to the y-axis at all! There must be also a T force that when it gets high enough it will break the rope. Can someone explain them to me? In this scenario does the T force of the rope being related to the centripetal force?

 

[vanhees71]

What's wrong with my suggestion in #2? It's really not more to the kinematics of circular motion than this very simple mathematical exercise!

 

[babaliaris]

What's wrong with my suggestion in #2? It's really not more to the kinematics of circular motion than this very simple mathematical exercise!

x(t)=r[excos(ωt)+eysin(ωt)]

I can't understand how to relate the formula above with the forces. Also its a little hard for me to understand what the formula actually describes. Probably an orbit around the circle (position)? Maybe because I don't think "multidimensionaly"? I see a force (pulling the particle towards the center of the circle) and I'm wondering why it does not moving towards the center? Is it because I'm thinking that the force is being applied in on dimension? Please also consider the sketch i uploaded in #11

 

[vanhees71]

Ok, so maybe I did not understand at which level you are studying. You marked the thread as to be I level. So I assumed you know vectors and calculus.

$\vec{x}(t)$ describes the trajectory of the particle in 3D space, i.e., it gives the position in terms of a vector pointing from some fixed origin of your reference frame as a function of time. If you take a Cartesian basis system $\vec{e}_j$ ($j \in \{1,2,3 \}$), i.e., three unit vectors that are mutually perpendicular to each other, you can describe the vector by three real numbers, its components with respect to this Cartesian basis, which are functions of time:
$$\vec{x}(t)=\sum_{j=1}^3 x_j(t) \vec{e}_j.$$
Now the motion along a circle with constant angular velocity $\omega$ is described by the above given formula
$$\vec{x}(t)=r [\vec{e}_1 \cos(\omega t) + \vec{e}_2 \sin(\omega t)], \quad r>0 \quad \text{constant}.$$
Now the 1st derivative with respect to time gives the velocity,
$$\dot{\vec{x}}(t)=\vec{v}(t)=r \omega [-\vec{e}_1 \sin(\omega t) + \vec{e}_2 \cos(\omega t)].$$
The second derivative is the acceleration
$$\ddot{\vec{x}}(t)=\dot{\vec{v}}(t)=\vec{a}(t)=-r \omega^2 [\vec{e}_1 \cos(\omega t) + \vec{e}_2 \sin(\omega t)]=-\omega^2 \vec{x}(t).$$
Now according to the 2nd law, this implies that you need a force
$$\vec{F}=m \vec{a}=-m \omega^2 \vec{x}.$$
This tells you that the force has magnitude $$F=|\vec{F}|=m \omega^2 r=\text{const}$$, and at any instant of time points radially inwards, i.e., the force pulls the mass instantly towards the origin of the coordinate system, around which it rotates, to keep it on its circular orbit.

 

[babaliaris]

Ok, so maybe I did not understand at which level you are studying. You marked the thread as to be I level. So I assumed you know vectors and calculus.

$\vec{x}(t)$ describes the trajectory of the particle in 3D space, i.e., it gives the position in terms of a vector pointing from some fixed origin of your reference frame as a function of time. If you take a Cartesian basis system $\vec{e}_j$ ($j \in \{1,2,3 \}$), i.e., three unit vectors that are mutually perpendicular to each other, you can describe the vector by three real numbers, its components with respect to this Cartesian basis, which are functions of time:
$$\vec{x}(t)=\sum_{j=1}^3 x_j(t) \vec{e}_j.$$
Now the motion along a circle with constant angular velocity $\omega$ is described by the above given formula
$$\vec{x}(t)=r [\vec{e}_1 \cos(\omega t) + \vec{e}_2 \sin(\omega t)], \quad r>0 \quad \text{constant}.$$
Now the 1st derivative with respect to time gives the velocity,
$$\dot{\vec{x}}(t)=\vec{v}(t)=r \omega [-\vec{e}_1 \sin(\omega t) + \vec{e}_2 \cos(\omega t)].$$
The second derivative is the acceleration
$$\ddot{\vec{x}}(t)=\dot{\vec{v}}(t)=\vec{a}(t)=-r \omega^2 [\vec{e}_1 \cos(\omega t) + \vec{e}_2 \sin(\omega t)]=-\omega^2 \vec{x}(t).$$
Now according to the 2nd law, this implies that you need a force
$$\vec{F}=m \vec{a}=-m \omega^2 \vec{x}.$$
This tells you that the force has magnitude $$F=|\vec{F}|=m \omega^2 r=\text{const}$$, and at any instant of time points radially inwards, i.e., the force pulls the mass instantly towards the origin of the coordinate system, around which it rotates, to keep it on its circular orbit.

LOL. I'm a university student and I know calculus and vectors. The problem was in the symbols (I'm such an indiot :p ). Because in greece we use i,j and k as the normalize vectors of the Cartesian system I did not realize that e1 and e2 was actually the normalize vectors (did't even noticed the arrows above them) and thus i did not understand that the formula was actually producing a vector... And i was saying to myself "how can a scalar size give the position of an orbit?" Now i understand! I really appreciate your help! I can't understand why the book is hiding this formula, everything seems much easier now.

 

[babaliaris]

So, can you know explain why when you are spinning a particle that is tied in a rope (so the particle is doing a uniform circular motion) why it does not fall to the ground due to it's weight? Also if the speed of the uniform circular motion is big enough it can break the rope, why is that? Also i want to ask something else. In the book: a = v^2 / R (this is the magnitude only) .The ω which u use in the formula above is something else than V? Why the book does not mention something about ω when it should?

 

[vela]

So, can you know explain why when you are spinning a particle that is tied in a rope (so the particle is doing a uniform circular motion) why it does not fall to the ground due to its weight?

Consider a projectile. The only force on it, the force of gravity, points down, but it doesn't fall straight down as you seem to suggest the spinning particle should. Why is that?

 

[babaliaris]

Consider a projectile. The only force on it, the force of gravity, points down, but it doesn't fall straight down as you seem to suggest the spinning particle should. Why is that?

I don't know The projectile moves horizontally with a constant velocity but vertically accelerates with a = -g, so it will hit the ground sometime. The spinning particle accelerates all the time and moves in an orbit where it's velocity changes due to the acceleration. Maybe this is the reason? But there is no way to see it with mathematics? I can't just believe words... There's must be a force on the particle except it's weight (Fg) so ∑ƒy = 0 ⇔ -m⋅g + F = 0 ⇔ F = m⋅g and maybe this F has to due something with the Centripetal force. Probably I'm wrong but this the most logical thing to think of.

Or better, take this example:

When the ball is upside down then the forces which are being applied to it are it's weigh, the normal force and the centripetal force so : -ƒc - m⋅g - ƒn = m⋅ay, in other words if the ball does not fall it means ay ≠ 0 and actually ay > 0. According to Newton if there is an ay > 0 (towards the sky) then it must be also a force in the same direction in such a way -ƒc - m⋅g - ƒn + F = 0 <=> F = ƒc + m⋅g + ƒn

Honestly I can't think of something else...

 

[CWatters]

Your answer make's the most sense now (i finished reading about uniform circular motion), but still i can't understand a few things. It's weird, i reached so far learned about motions, forces, Newton's laws and now I've stuck... When a particle move's in a uniform circular motion there is a Centripetal force towards the center.

Here is how I like to explain it...

Consider a particle moving in a straight line. To deflect it off course slightly you need to give it a brief sideways force/nudge. Afterwards its still moving in a straight line but in a different direction. Give it another nudge and it changes direction again. With care you could make it move in a square pattern, pentagon, hexagon or octagon. The more sides the shape has the more nudges you need to give it and the more frequently you need to give them. In the extreme (eg a circle) you need to give it a constant sideways force. This is called the centripetal force.

You can calculate the centripetal force _required_ to move in a circle of radius r at velocity v...

F = mv²/r

Question 1:
So if we assume there is no gravity and no other forces applied on the particle, why the particle is not moving towards the center of the circle?

If you apply a force greater than mv²/r to the particle it WILL move toward the centre. You can rearrange the equation to..

r = mv²/F

If F increases the radius r reduces. If F reduces the radius r increases.

Note that F is the net force on the particle. In some cases the net force has two components, gravity might be one and string tension or normal force from a track the other.

 

[CWatters]

So, can you know explain why when you are spinning a particle that is tied in a rope (so the particle is doing a uniform circular motion) why it does not fall to the ground due to it's weight? Also if the speed of the uniform circular motion is big enough it can break the rope, why is that? Also i want to ask something else. In the book: a = v^2 / R (this is the magnitude only) .The ω which u use in the formula above is something else than V? Why the book does not mention something about ω when it should?

You mean spin it in a vertical circle?

At all times the net force must be mv²/r otherwise it won't move in a circle.

At the top "Falling down" requires the radius to reduce. In order for that to happen the centripetal force must be greater than mv²/r.

That will happen if gravity provides too much centripetal force. Another way to say the same thing is... Gravity will provide too much centripetal force (and it will fall) if the velocity is too slow.

 

[Bandersnatch]

In the book: a = v^2 / R (this is the magnitude only) .The ω which u use in the formula above is something else than V?

ω is angular velocity. It's often used in problems dealing with circular motion. Just as regular velocity is the change in distance over time, ω is the change in angle over time.
The relationship between the two is $V = ωR$.
Best to visualise by considering a particle going around in a circle of radius R, with the period of one full rotation being T. Then the magnitude of its velocity is the distance covered in one rotation ($d=2πR$) over the period T. I.e., $V=\frac{2πR}{T}$.
At the same time, you can say that its angular velocity is the angle covered in one rotation (ε = 360 degrees, or 2π in radians) over one period T. I.e. $ω = \frac{2π}{T}$
Divide V by ω to get to the $V = ωR$. Which is intuitively right, since if you want to cover the same angle per unit time in a larger circle, you need to go at higher speed.

 

[CWatters]

Also if the speed of the uniform circular motion is big enough it can break the rope, why is that?

To go fast requires a large centripetal force because the required centripetal force is proportional to v squared. Most of it is provided by tension in the string. At the bottom string tension has to counter gravity AND provide the centripetal force. At the top gravity helps provide some centripetal force so it's more likely to fail at the bottom.

 

[Delta2]

Your answer make's the most sense now (i finished reading about uniform circular motion), but still i can't understand a few things. It's weird, i reached so far learned about motions, forces, Newton's laws and now I've stuck... When a particle move's in a uniform circular motion there is a Centripetal force towards the center.

Question 1:
So if we assume there is no gravity and no other forces applied on the particle, why the particle is not moving towards the center of the circle? So if I name r the axis where the Centripetal force is lying , according to Newton's second law:

∑ƒr = m⋅a ⇔ -ƒc = m ⋅ ( -v^2 / R ) ⇔ fc = m ⋅ ( v^2 / R ) but still i can't understand why the parcicle is moving in a circle and not towords the center. If you can use maths to explain use them.

Question 2:
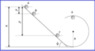
Let's say i have a rope tied in a particle and I'm spinning it (around a y axis) with my hand. Then the particle is entering a uniform circular motion but also it does not fall to the ground and according to Newton there must be another force with the same magnitude as Fg (weight) in the opposite direction so the particle won't move at all on the y axis. Also if i speed faster and increase the constant speed of the uniform circular motion, the rope will break. Consider the following sketch:

I have a really hard time understanding the cause of these forces. It must F = -Fg so the particle won't fall to the ground or actually won't move to the y-axis at all! There must be also a T force that when it gets high enough it will break the rope. Can someone explain them to me? In this scenario does the T force of the rope being related to the centripetal force?

A particle's acceleration $\vec{a}$ can be split to two components $\vec{a}(t)=\vec{a}_{tan}(t)+\vec{a}_c(t)$.

1)$\vec{a}_{tan}(t)$ is the component of acceleration that is always (at any instant of time) parallel to the vector of velocity, and what it does is to change the magnitude of the vector of velocity. It is called tangential acceleration. This component cannot change the direction of the velocity vector, simply because it is always, that is at any instant of time parallel to the velocity vector and we know when an acceleration is parallel to velocity, all it does is to change the magnitude of velocity.

2)$\vec{a_c}(t)$ is the component of acceleration that is always perpendicular to the vector of velocity, and what it does is to change the direction of the vector of velocity. It is called centripetal acceleration. This component cannot change the magnitude of the velocity vector simply because it is always, that is at any instant of time perpendicular to the vector of velocity.

I understand that the way I split the total acceleration and the comments of 1) and 2) are not fully mathematically rigorous (for example you might ask, why the centripetal acceleration changes the direction of the velocity vector and only that). If you want the full mathematical reasoning, I ll provide it, just ask.

In uniform circular motion, the magnitude of tangential acceleration is constant and zero. The magnitude of centripetal acceleration is as you know , constant $\frac{v^2}{R}$ and post #14 very successfully illustrated all the math behind its calculation.

The equation that must hold between centripetal and tangential acceleration so that we have circular (uniform or non uniform motion) is

$|\vec{a}_c(t)|=\frac{({\int |\vec{a}_{tan}(t)|dt})^2}{R} (1)$

for some constant R (I can provide the math of how we arrive at this equation, it is a generalization of what vanhees71 does at post#14).

So :
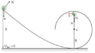
Question 1: The only acceleration is centripetal acceleration, that is always (that is at any instant of time), vertical to the vector of velocity, so all that can do is just change the direction of the velocity vector and not its magnitude. Notice that centripetal acceleration here, is not the same as the vertical acceleration in a particle that does projectile motion. In the projectile case the gravitational acceleration is vertical to velocity only at the start, so it acts as centripetal acceleration only at start, but afterwards the gravitational acceleration it can be split to two components, one tangential and one centripetal. The reason that it doesn't do circular motion is that if you do analyse the force and the acceleration into tangential and centripetal component you ll find that equation (1) cannot be satisfied for some constant R, R has to be time varying.

Question 2: In this case, both the centripetal acceleration and the tangential acceleration are time varying. The particle does non uniform circular motion.
if we do analyze the forces correctly into parallel and perpendicular to the velocity, components, we ll find that the tangential acceleration is $a_{tan}(t)=g\cos{\theta(t)}$. The centripetal acceleration is $a_c(t)=\frac{T(t)}{m}+g\sin{\theta(t)}$ where T(t) the tension of the string which will be time varying. Why equation (1) is true in this case? The key is the tension of the string, which can change and adjust itself so that equation (1) is satisfied. Of course if that integral in (1) (which is essentially the time varying magnitude of velocity)becomes two big then the string might break because it will not be able to supply such a big T(t).. or if it becomes two small, then T(t) might have to become radially outwards (we know that a string can supply only a radially inwards force).

 

[A.T.]

i can't understand why the parcicle is moving in a circle and not towords the center.

Do you understand the difference between velocity and acceleration? Accelerating towards the center is different from moving towards the center.

Can someone explain them to me? In this scenario does the T force of the rope being related to the centripetal force?

If it moves in a circle the net force is the centripetal force mv²/r, and the string tension will be whatever is needed for that.

 

[vanhees71]

I think you need to study vector algebra and analysis once again. This is really very basic stuff, and without this mathematical prerequisites there's no way to learn physics on the university level (in my opinion not at any adequate level)!

 

[babaliaris]

Guys thank you very much! I understood everything! The problem was not in lack of mathematical concepts but because I was probably overthinking and overcomplicating things too much. I was thinking that the direction of forces define the direction of the motion something that of course is wrong. Then i started thinking one by one what is a force, what is acceleration and what is velocity and by combining them with your answers I finally got over the overthinking. So this is my conclusion:

1) A force is just a property which when it exist's in an object with mass, then this object accelerates.
2) Velocity is the change of distance over time.
3) Acceleration is the change of Velocity (change in direction or magnitude or both).

Key Problem: FORCES DO NOT SHOW THE DIRECTION OF THE MOTION (I was overthinking to much obviously , reading a lot of hours too because I'm hungry to learn!)

So a particle that is moving straight with a constant speed does not change directions. In a uniform circular motion, the particle must accelerate all the time so velocity will always change in direction but not speed. The particle does not fall on the ground, because if it was then it means that is not in a uniform circular motion or in other words the velocity has changed in direction in such a way that now the direction of the Velocity is always pointing downwards, but this can only happen when there is no centripetal acceleration so the direction of the particle's velocity won't change over time but remains towards the ground due to a = -g acceleration.

 

[babaliaris]

Now I have one more question. Consider the following:

The ball is upside down. The information which i have is:
1) The speed of the ball (lets say that the speed is constant when it starts the circular motion).
2) The mass of the ball.
3) The radius of the circle.

Find the normal force when the ball is upside down.

According to the book, the only things that i can calculate so far (what i learned in physics so far) is ONLY the magnitude of the centripetal force and the weight of the ball. Because in this situation all the forces are parallel to the y-axis and point downwards i can write:
-m⋅g - Fn = m⋅(-u^2 / R)

I know everything except Fn so i can calculate it. Now the book does not showing other situations, maybe because i don't have the knowledge yet, but what if I was analyzing the same problem when the ball was a little more to the right than it is now.

In this situation i know that weight = -m⋅g but I don't know the direction of the acceleration. I can calculate the magnitude but how am i going to find the direction? If i just knew the angle of the centripetal acceleration with the x-axis i could calculate the vector but now can i do something? Or the exercise should give me one more information, perhaps the angle of a with x at that point.

 

[FactChecker]

The diagram looks like the initial height, h, is equal to 2R. Is that true? If you know you can figure out the velocity, v, by conservation of the initial energy. Otherwise, you would need to express v as a function of the variable h, v(h).

I don't understand your question about the acceleration of gravity. It is down. When the ball is at the top, the centrifugal acceleration is up and the acceleration of gravity is directly opposite.

 

[vanhees71]

In this question, there's no reason to got into non-inertial frames. Just stay in the "lab frame", and there's no centrifugal force (but a centripetal force!).

 

[babaliaris]

Sorry guys my mistake, i gave you wrong image.

In the second (i forgot to draw the Velocity vector but the particle is doing uniform circular motion inside a ring), a should have the same direction as Fn (towards the center) but i can only calculate the magnitude of a = v^2 / R and thus i can't find Fn because i don't have enough info about the a vector. (Also in Newtons second law i forgot to put an arrow above a at the bottom of the page and Fn, a and Fn are vectors there)

 

[Delta2]

The vector of centripetal acceleration at a point has always the direction of the radius at that point. So in your scheme, the vector of centripetal acceleration points towards the center, has the same direction as $\vec{F_N}$.

 

[babaliaris]

The vector of centripetal acceleration at a point has always the direction of the radius at that point. So in your scheme, the vector of centripetal acceleration points towards the center, has the same direction as $\vec{F_N}$.

Yes but i don't know Fn I want to calculate it. Please also consider #30 (because i provided you with the wrong image on #27)

 

[Delta2]

yes I war referring to the second scheme in post #30. The centripetal acceleration there has the same direction as $\vec{F_N}$. But the total acceleration which is $\vec{a}=\vec{a}_{tangential}+\vec{a}_{centripetal}$ makes an angle with the x-axis which you can calculate, together with the calculation of $F_N$

 

[babaliaris]

yes I war referring to the second scheme in post #30. The centripetal acceleration there has the same direction as $\vec{F_N}$. But the total acceleration which is $\vec{a}=\vec{a}_{tangential}+\vec{a}_{centripetal}$ makes an angle with the x-axis which you can calculate, together with the calculation of $F_N$

I can't understand

This is where i reached so far:

I know v, m, r and g but not theta. I need theta to calculate the final result...

[Edited]
LoL actually i can find the magnitude of Fn when the particle is upside down and then in the formula above a can replace Fn = |Fn| (cos8 i + sin8 j) and now i have to find (cos8 i + sin8 j) . This is what you meant (8 = theta symbol)

 

[Delta2]

First of all $\Theta$ can be calculated if you know the height h of that point, it will be $\sin\Theta=\frac{h}{R}$

Your equation is correct at start but at some point it goes wrong. The total acceleration is not only the centripetal acceleration. There is tangential acceleration too. You correctly expanded centripetal acceleration to its i, j components, but you need to add the tangential acceleration components too. So you missing two terms. You also forgot to write g as $g\vec{j}$.

 

[babaliaris]

Never heard of tangential acceleration yet. I just know that a particle that is doing uniform circular motion has only one acceleration, the centripetal acceleration. This is what the book told me so far. Next chapter is kinetic energy.

 

[Delta2]

Never heard of tangential acceleration yet. I just now that a particle that is doing uniform circular motion has only one acceleration, the centripetal acceleration.

Very well, but in the situation you examining at post #30, the particle does non-uniform circular motion... that's the whole "catch"... So better to avoid this problem till you learn about tangential acceleration.

 

[babaliaris]

I see... I will wait then until i reach the appropriate chapter. Once again I'm rushing

 

[CWatters]

+1

It's not often you need to calculate the net acceleration when the motion is non-uniform. Try easier problems first.

 

[vanhees71]

Again, math is your friend. If I understand the problem right, you have a circular loop in the $x_1 x_2$ plane. For convenience I put its center in the origin of the coordinate system. The gravitational acceleration is $\vec{g}=-g \vec{e}_y$. Now the motion on the circular loop most simply is described with polar coordinates,
$$\vec{r}=r \cos \phi \vec{e}_1 + r \sin \phi \vec{e}_2.$$
The equation of motion is
$$m \ddot{\vec{r}}=m \vec{g} \, \Rightarrow \, \ddot{\vec{r}}=\vec{g}.$$
The only thing you need is the 2nd derivative wrt. time.

Then fortunately the force is conservative, i.e., it has a potential
$$V(\vec{r})=-m \vec{g} \cdot \vec{r}=m g x_2=m g r \sin \phi.$$
Now energy is conserved, i.e.,
$$E=\frac{m}{2} \dot{\vec{r}}^2+m g r \sin \phi=\text{const}.$$
With the chain rule (and because $r=\text{const}$) you have
$$\dot{\vec{r}}=-r \dot{\phi} \sin \phi \vec{e}_1 + r \dot{\phi} \cos \phi \vec{e}_2$$
and
$$\dot{\vec{r}}^2=r^2 \dot{\phi}^2.$$
Now it should be very easy to solve your problem, using the energy conservation law above.

 

[A.T.]

Never heard of tangential acceleration yet.

Have you heard of Wikipedia?
https://en.wikipedia.org/wiki/Acceleration#Tangential_and_centripetal_acceleration

 

[babaliaris]

Have you heard of Wikipedia?
https://en.wikipedia.org/wiki/Acceleration#Tangential_and_centripetal_acceleration

Yes but anyway, it's very early for me right now. I just started with physics and I was rushing.

 

[Friend of Kalina]

1. The ball on the string doesn't fall to the center because it starts with a velocity tangent to the circle. The string pulls it into the center of the circle, the velocity imparts an inertial component to keep going straight, the result is that the ball turns along the circumference of the circle.

2. The ball doesn't fall to the ground because the string is holding it up. If you stand to the side, you will see that the string is not parallel to the ground, but is instead at an angle. The total force on the string is composed of the horizontal acceleration, keeping the ball going in a circle, and the vertical acceleration countering gravity. The flatter you keep the string, the higher the force required; centripetal force is linked by the angle of the string, but also increases, and the ball goes faster.

Oops. Somehow failed to notice I was still on page 1 of 3 and that question had been resolved. Sorry.

 

[PeterO]

I'm in the chapter of Uniform Circular Motion and I have a hard time understating centipetal acceleration. Until now I knew that acceleration describes "how fast velocity changes in magnitude" except projectile motion because when it reaches maximum height then g is going to change the direction on the Vy and make it move downwards but now in this kind of motion, acceleration describes only "how fast the direction of the velocity changes" and not the magnitude. Ok I understand that but what I really don't understand is when I'm in a car and take a turn I feel pushed in the opposite direction of the circles center. But acceleration is pointing at the center of the circle

You probably have the answer but...
When a car accelerates forward, you feel like you are being pushed, back into the seat.
When a car brakes heavily in an emergency stop (it is accelerating back) you feel you are being thrown forward,
Why should it feel unusual that when a truning car is accelerating towards the centre of the circle (centripetal acceleration) you feel like you are being thrown outwards, away from the centre.
The real truth is that you are not being pushed or thrown in any of those directions - it just feels like you are. We are often deceived. We can even feel (momentarily) lighter when an elevator starts to move, then (momentarily) heavier when it stops again.

 

[vanhees71]

You probably have the answer but...
When a car accelerates forward, you feel like you are being pushed, back into the seat.
When a car brakes heavily in an emergency stop (it is accelerating back) you feel you are being thrown forward,
Why should it feel unusual that when a truning car is accelerating towards the centre of the circle (centripetal acceleration) you feel like you are being thrown outwards, away from the centre.
The real truth is that you are not being pushed or thrown in any of those directions - it just feels like you are. We are often deceived. We can even feel (momentarily) lighter when an elevator starts to move, then (momentarily) heavier when it stops again.

No! What you feel in the car is that you get pushed forward by the force imposed on you by the seat!

It's the same thing in a merry-go-around: You feel the push of the force imposed on you by the seat towards the center of the circle, i.e., the centripetal force.

 

[A.T.]

No! What you feel in the car...

"Feel" can mean different things:
- Direct sensation of contact forces (what you probably mean)
- Interpretation of your movement relative to the car (what Peter probably means)

 

[vanhees71]

Maybe a physicist "feels" differently from being trained to think differently. ;-)).

 

[rcgldr]

In a carnival scrambler ride, there's a lot of centripetal acceleration, but 2 people sit side by side in the ride with no seat belts. If the riders end up pushing against each other, the outside rider exerts a centripetal force on the inside rider, and the inside rider exerts a centrifugal reaction force to the outside rider. This is one example where a centrifugal reaction force can be felt.

 

[PeterO]

No! What you feel in the car is that you get pushed forward by the force imposed on you by the seat!

It's the same thing in a merry-go-around: You feel the push of the force imposed on you by the seat towards the center of the circle, i.e., the centripetal force.

I am quite aware of what forces are actually acting on you - I was using "feel" as the sensation you experience. Indeed if you watch an unbelted child sitting in the back seat of the car they do not feel a centripetal force from the seat - they eventually feel the centripetal force from the door when the have finally tumbled that far. They don't know to hang on - especially if they have been brought up to always wear a seat belt and have just omitted this time. The seat belt can supply the centripetal force need without the "outward tumble" - which is, I know, just continuing (approximately) in a straight line.
By the way, another way to make the seat push forward on you is to have someone else push you into the seat - while the car is stationary. It that case you still don't notice the seat pushing, but wonder why the person is pushing you. When the car accelerates, you still don't notice the seat pushing, you just wonder who is pushing you into the seat this time. One reason to study Physics is so you can explain that there is nothing pushing you into the seat, it is just a ficticious force that has appeared in the non-inertial frame you have briefly found yourself in.

 

[rcgldr]

there is nothing pushing you into the seat, it is just a fictitious force that has appeared in the non-inertial frame you have briefly found yourself in.

When a car is accelerating, you have a Newton 3rd law pair of forces, the seat exerts a forwards force on the person, the person exerts a reaction force on the seat. The reaction force is a real force in any frame of reference.

Using the car as an accelerating frame of reference, the fictitious force is the force that would appear to accelerate a body in "free fall" with respect to the accelerating frame of reference, and would not be part of a Newton 3rd law pair of forces. The Newton 3rd law pair of forces are still the same, seat exerts forward force on person, person exerts backwards force on seat.