maistral
- 235
- 17
Hi. I have this Bessel look-a-like DE (however it has the negative sign on the dependent variable):
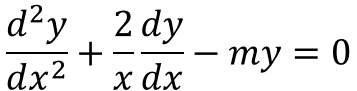
My attempt at a solution is by (obviously) trying to transform it into a Bessel DE by multiplying it with x2 on both sides, then it would look like the Spherical Bessel differential equation, except that there's that negative sign beside y.
Then what? I have no idea what to do. Can someone tell me what this DE is supposed to look like so I can solve it on my own?
I have no idea what to do. Can someone tell me what this DE is supposed to look like so I can solve it on my own?
My attempt at a solution is by (obviously) trying to transform it into a Bessel DE by multiplying it with x2 on both sides, then it would look like the Spherical Bessel differential equation, except that there's that negative sign beside y.
Then what?
 I have no idea what to do. Can someone tell me what this DE is supposed to look like so I can solve it on my own?
I have no idea what to do. Can someone tell me what this DE is supposed to look like so I can solve it on my own?