MissBisson
- 24
- 0
Homework Statement
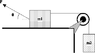
A 27.1 kg block (m1) is on a horizontal surface, connected to a 6.70 kg block (m2) by a massless string as shown in the figure below. The frictionless pulley has a radius R = 0.097 m and a moment of inertia I=0.070 kgm2. A force F = 213.7 N acts on m1 at an angle theta = 34.5°. There is no friction between m1 and the surface. What is the upward acceleration of m2?
Homework Equations
Torque = F x R
Torque = I x alpha
a = R x alpha
I = 1/2 m x R^2
The Attempt at a Solution
Block 1 : Fcos(theta) - T1 = m1a T1 = Fcos(theta) - m1a (opposite direction of accereration)
Block 2 : T2 - m2g = m2a T2 = m2a + m2g (in the direction of acceleration)
Torque = (T2-T1)R = I x (a/R)
(m2a + m2g - Fcos(theta) + m1a)R = 1/2 m x R^2 x (a/R)
m2a + m2g - Fcos(theta) + m1a = (m x R^2 x a)/(2 x R^2) R^2 cancel out
m2a + m2g - Fcos(theta) + m1a = (m x a)/2
m2a + m1a - (m x a)/2 = Fcos(theta) - m2g
a (m2 + m1 - m/2) = Fcos(theta) - m2g
a = (Fcos(theta) - m2g)/(m2 + m1 - m/2) -----------------> A
a = (213.7cos(34.5) - 6.7*9.81)/ (6.7 + 27.1 - 17.88/2)
a = (110.39/26.36)
a= 4.187m/s^2
I know that the answer is 2.68m/s^2 and that the equation A should be
a = (Fcos(theta) - m2g)/(m2 + m1 + m/2)
But i don't know how to get that...