Use a GEOCENTRIC reference frame to explain the earth's orbit

[stunner5000pt]

Yes i understand that i posted this earlier, but it was perhaps just glanced over since it had got replies (by me trying to bump it up, sorry, again). But i seriously would like to know how to solve this question ANy help would be appreciated

Note that i have copiedd the question exactly from the test!

Given the sun's mass (Ms = 2 x 10^30 kg) then Earth sun distnace (1.5 x 10^11 m) Newtons Constant G = 6.7 x 10^-11 Nm^2 kg^-2 use a GEOCENTRIC reference frame to explain the Earth's orbit (approcximate as a circle)

This was a question on my test and at first sight i was shocked.

But geocentric... if geocentric then the Earth would be at the centre and the sun would revolve around the sun. Would the sun have its own circular orbit around orbit as well?

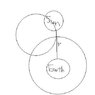
So far i have been thinking and thinking (and thinking...) i have no clue. Would the diagram for this look like the one posted here?
this is my effort so farr

the force between the sun an the Earth is
F_{g} = G \frac{m_{sun} m_{earth}}{r^2}

the centripetal force of the sun is F_{C1} = m_{sun} \frac{v_{1}^2}{r_{1}}

But since the sun is revolving around some axis it also experiences anotehr centripetal force F_{C2} = m_{sun} \frac{v_{2}^2}{r_{2}}

equate all those toegether when the sun is at the max distance
G \frac{m_{earth}}{r} + v_{1}^2 + v_{2}^2 = 0

and when the minimum distance is taken
G \frac{m_{earth}}{r} + v_{1}^2 - v_{2}^2 = 0

thus v_{2}^2 = -v_{2}^2
thus v2 = 0?? Is this good enough?? Is this valid??

i am really supposed to take the Ptolemean system like i have? Or have i lost the point of the question??

 

[cepheid]

Okay...let's take a look at your conceptual understanding of the problem before we tackle anything else. The geocentric reference frame shouldn't be too hard, considering we're in it! So, to us, what does the sun appear to do? Revolve around us in a roughly circular orbit once every ~365 days...right? That's about it. So, let's look at that diagram: you have two circles drawn (not including the celestial bodies). One of them is centred on the Earth. What does it represent? Then, strangely, you have drawn another circle centred on the sun. For the life of me, I cannot figure out what it is. It would be very helpful to me if you could explain your thinking. Also, I've attached my (very crude diagram). What do you, (or anyone else) think of it?

 

[HallsofIvy]

As long as you are only considering the Earth and the sun, a geocentric viewpoint is as easy as heliocentric. Instead of the Earth rotating around the sun in a circle of radius 93 million miles, the sun rotates around the Earth in a circle of radius 93 million miles.

 

[stunner5000pt]

i drew the sun orbiting something while in its orbit because isn't that how they explained the different phases of the year with the ptoleman system?? I thought that that is what had to be done.

SO then all i have to do is simply show the sun rotates around the Earth but how does that explain the rotation of the Earth itself?
\