Use of Bernoulli equation for pumps

[Soren4]

I have a doubt on the use of Bernoulli equation for pumps. Consider the situation in the picture.

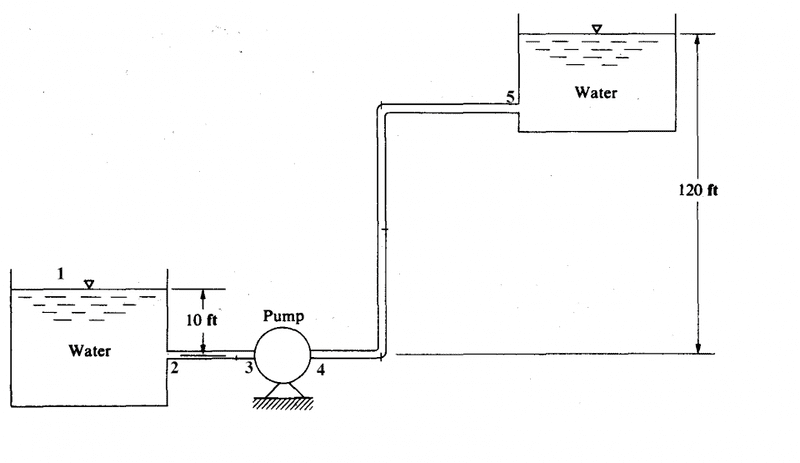
I marked different points: $1$ on the surface of first tank, $2$ in the exit from first tank, $3$ just before the pump, $4$ just after the pump and $5$ entering the second tank.
Now consider Bernoulli equation in the "normal form" (ignoring the pump)
$$p_a+\frac{1}{2} \rho v_a^2 +\rho g h_a=p_b +\frac{1}{2} \rho v_b^2 +\rho g h_b\tag{1}$$
And in the form for the presence of pump delivering power $\mathscr{P}$
$$(p_a+\frac{1}{2} \rho v_a^2 +\rho g h_a) Q +\mathscr{P}=(p_b +\frac{1}{2} \rho v_b^2 +\rho g h_b) Q \tag{2}$$
$a$ and $b$ are two generic points among the ones listed above.

My question now is: can I use $(2)$ between any point before the pump and any point after the pump, regardless the height, velocity and pressure in such points?
I have this doubt because usually one takes point $1$ and $5$ and uses $(2)$ - and I'm ok with that- but, if the answer to previous question is yes, I could also choose to use $(2)$ between $1$ and $4$ or $2$ and $5$ or $2$ and $3$ and so on and that sound strange because the quantity $p+\frac{1}{2} \rho v^2 +\rho g h$ should be the same before and after the pump, indipendently from the particular point chosen. In other words I should be able to use $(1)$, normal Bernoulli equation, between $1$ and $2$, which is not very realistic, since the fluid in $2$ will probably move with a velocity that is influenced by the pump.

That is, even if $2$ is before the pump, the velocity there is different from the situation with no pump. And that's what I cannot understand here. How is that possible? And can I use $(1)$ between $1$ and $2$?

Any suggestion is highly appreciated.

 

[Tazerfish]

There is one slight problem. friction.If your system was frictionless and point a is before trhe pump and b is after it, I suspect the equation would be correct.
(for any points a and b which satisfy these conditions)
But because of the friction there is going to be more (whatever the units are called) "upstream" in your equation.
The specific energy at 4 will be higher than the specific energy at 5.(ignoring heat)
Adding a friction term into the equation would probably fix that.
EDIT: Why exactly do you want to know that?
Do you want to build soething or is it a theoretical consideration ?

 

[rcgldr]

Power is work done or change in energy per unit time. Bernoulli equation is energy per unit volume, without a time factor. Power can't be combined with Bernoulli as shown. You'd need a flow rate (volume per unit time) to multiply the Bernoulli equation into an equation of power.

I missed the Q factor, which is the flow rate.

 

[jack action]

In other words I should be able to use $(1)$, normal Bernoulli equation, between $1$ and $2$, which is not very realistic, since the fluid in $2$ will probably move with a velocity that is influenced by the pump.

That is, even if $2$ is before the pump, the velocity there is different from the situation with no pump. And that's what I cannot understand here. How is that possible? And can I use $(1)$ between $1$ and $2$?

Yes, the fluid will move at $(2)$ because of the pump, but the pressure will also drop (according to $(1)$).

Think about it: If the static pressure would remain the same, how would the fluid from the tank accelerate into the pipe to gain speed? $ma = \Delta F = \Delta PA$

 

[rcgldr]

Assuming no losses from the pipes, the standard Bernoulli equation can be used before or after the pump, just not across the pump.

 

[Tazerfish]

My question now is: can I use (2) between any point before the pump and any point after the pump, regardless the height, velocity and pressure in such points?

I think we agree, that yes you can use it like that.(If you ignore friction)

In other words I should be able to use (1), normal Bernoulli equation, between 1 and 2, which is not very realistic, since the fluid in 2 will probably move with a velocity that is influenced by the pump.

I think it is realistic.
The pump only produces lower pressure. It does no direct work on the fluid its puling in.
The velocity will increase at the "cost" of the pressure.

It confuses me a little that the pumps seems to not do any work on the fluid it is "sucking" in.
That certainly holds up(again ignoring friction) if you look at a pump that sucks in a given volume and pushes it out somewhere else but when you consider an more "open" pump like a turbine I would be somewhat at loss.
Do thesee kinds of pumps still not do any work on the fluid they are sucking in( far away from the pump the answer is probably yes) ?
Where do you draw the line between the fuild that has been given the extra bit of energy by the pump and the fluid that hasn't ?

 

[Nidum]

A positive displacement pump working steady state can be modeled as a flow sink on the inlet side and a flow source on the delivery side .

Gets a bit more complicated for rotodynamic pumps .

.

 

[rcgldr]

It confuses me a little that the pumps seems to not do any work on the fluid it is "sucking" in.

The pump only performs work on the fluid within the pump. The pressure increase (sometimes called a pressure jump) times the volume flow rate equals the output power of the pump.

 

[Tazerfish]

The pump only performs work on the fluid within the pump. The pressure increase (sometimes called a pressure jump) times the volume flow rate equals the output power of the pump.

Yeah that is the conclusion I came to after thinking a bit about it.It is just very counter-intuitive for me.
Can you maybe answer my previous question ?

...but when you consider an more "open" pump like a turbine...

Where do you draw the line between the fuild that has been given the extra bit of energy by the pump and the fluid that hasn't ?

Is the pressure jump more like a pressure gradient in these cases ?
Is that consideration even relevant in any way ?

 

[jack action]

Why do you think a turbine-like pump performs work on the fluid before its entrance? Is it because the fluid speeds up? Because the energy to accelerate the fluid comes from its static pressure which decreases as the speed increases. The result is no added energy to the fluid. Just like as if it was a convergent nozzle.

The energy begins to increase when the fluid enters the first rotor-stator assembly.

 

[rcgldr]

The pump only performs work on the fluid within the pump. The pressure increase (sometimes called a pressure jump) times the volume flow rate equals the output power of the pump.

Is the pressure jump more like a pressure gradient in these cases ? Is that consideration even relevant in any way ?

Within the pump there's a pressure gradient, in this case increasing from the inlet to the outlet. It doesn't matter where in the internals of the pump that the pressure increases, only that the pump maintains a pressure difference between the inlet port and the outlet port.

Since mass flow is constant within the pump, and assuming no compression (no change in density), and that the inlet and outlet ports are the same size, then the volume flow through the pump is constant and only the pressure increases.

Because the energy to accelerate the fluid comes from its static pressure which decreases as the speed increases. The result is no added energy to the fluid.

If anything, it is the pressure differences that cause acceleration. Stating the somewhat obvious, fluid accelerates away from a higher pressure zone towards a lower pressure zone. Bernoulli provides an equation that describes the relationship between velocity and pressure during the acceleration. Pressure is potential energy per unit volume, while 1/2 density velocity² is kinetic energy per unit volume. Bernoulli doesn't explain how pressure differential are created, only that they exist. In this case, the pump is responsible for creating and maintaining the pressure differences.

 

[jack action]

If anything, it is the pressure differences that cause acceleration.

[...]

In this case, the pump is responsible for creating and maintaining the pressure differences.

I'm not sure if we are saying the same thing, but I will state my POV in another way:

The pump accelerates the fluid inside the pump. The fluid «leaves» the inlet to go toward the outlet. This leaves an emptiness at the inlet, i.e no fluid ^[1]. The pressure at the inlet of the pipe will then push on the fluid in the pipe to accelerate it towards the pump inlet, attempting to create equilibrium once again. The result is a decrease in the pipe static pressure as no outside work was done on the fluid.

The point I'm trying to make is that the pump might create the conditions for the fluid being accelerated within the pipe, but the energy to do so does not come from the pump.

If there was not enough static pressure at the inlet of the pipe to convert to the desired dynamic pressure (given a pipe cross-sectional area), the expected mass flow rate will not be achieved and the pump would starved. Knowing that $p_o = \frac{1}{2}\rho v_{max}^2$ and $\dot m = \rho A v$, therefore $p_o \gt \frac{(\dot m / A)^2}{2\rho}$ is the ultimate lower limit for the static pressure to get the desired mass flow rate.

[1] Actually, pressure will drop, but it is just to picture the process.

 

[rcgldr]

The pump accelerates the fluid inside the pump.

From my prior post:

Since mass flow is constant within the pump, and assuming no compression (no change in density), and that the inlet and outlet ports are the same size, then the volume flow through the pump is constant and only the pressure increases.

At start up, there is acceleration of flow, but once the flow reaches steady state, then there's no net acceleration of fluid by the pump (flow rate out = flow rate in, assuming no change in density), just an increase in pressure.

 

[jack action]

«accelerates» was a bad choice of word from my part. «sets in motion» might have been better.