robot1000
- 5
- 0
I'm a bit stuck with using the C-N method
The question I'm trying to solve is the standard heat equation with:
U=[sin(pi)*x] at \tau = 0
& U = 0 at x = 0
& x = 1 for \tau \geq 0
The intervals are 0.2 in x AND 0.02 in \tau up to \tau = 0.06
I've been asked to solve using an Explicit which I've done using formula derived from the taylor theorem, but the second part is asking to use the C-N Method.
I started using this formula:
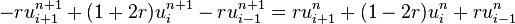 in matrix form, where I'm letting r = 0.5 using
in matrix form, where I'm letting r = 0.5 using
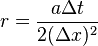
The only thing that's concerning me is that it seems a bit long winded and the answers for U(i,j) that have arisen don't seem at all close to the explicit method.
I put it all in matrix form and then using Gaussian elimination, is the correct method?
The question I'm trying to solve is the standard heat equation with:
U=[sin(pi)*x] at \tau = 0
& U = 0 at x = 0
& x = 1 for \tau \geq 0
The intervals are 0.2 in x AND 0.02 in \tau up to \tau = 0.06
I've been asked to solve using an Explicit which I've done using formula derived from the taylor theorem, but the second part is asking to use the C-N Method.
I started using this formula:
The only thing that's concerning me is that it seems a bit long winded and the answers for U(i,j) that have arisen don't seem at all close to the explicit method.
I put it all in matrix form and then using Gaussian elimination, is the correct method?