- #1
MarkFL
Gold Member
MHB
- 13,288
- 12
On another forum the following question was asked:
This was my initial reply:
Let:
$L$ = distance upstream to the safehouse
$W$ = width of the river
$v_s$ = swimming speed
$v_r$ = running speed
All variables above are assumed to be positive.
I have set it up as follows:
https://www.physicsforums.com/attachments/2775._xfImport
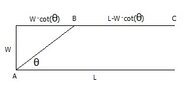
The prisoner swims from A to B and runs from B to C. The distance from A to B is:
\(\displaystyle AB=W\csc(\theta)\)
The time this takes is:
\(\displaystyle t_s=\frac{W}{v_s}\csc(\theta)\)
The distance from B to C is:
\(\displaystyle BC=L-W\cot(\theta)\)
The time this takes is:
\(\displaystyle t_r=\frac{1}{v_r}(L-W\cot(\theta))\)
The total time then is:
\(\displaystyle t=t_s+t_r=\frac{W}{v_s}\csc(\theta)+\frac{1}{v_r}(L-W\cot(\theta))\)
\(\displaystyle \frac{dt}{d\theta}=-\frac{W}{v_s}\csc(\theta)\cot(\theta)+\frac{W}{v_r}\csc^2(\theta)=W\csc(\theta)\left(\frac{1}{v_r}\csc(\theta)-\frac{1}{v_s}\cot(\theta) \right)=0\)
Observing \(\displaystyle \csc(\theta)\ne0\) for all real $\theta$, we then use:
\(\displaystyle \frac{1}{v_r}\csc(\theta)-\frac{1}{v_s}\cot(\theta)=0\)
\(\displaystyle \csc(\theta)\left(\frac{1}{v_r}-\frac{1}{v_s}\cos(\theta) \right)=0\)
\(\displaystyle \frac{1}{v_r}-\frac{1}{v_s}\cos(\theta)=0\)
\(\displaystyle \cos(\theta)=\frac{v_s}{v_r}\)
\(\displaystyle \theta=\cos^{-1}\left(\frac{v_s}{v_r} \right)\)
This is why I used variables, so we can make a few observations:
(1) the angle is independent of $L$ and $W$. We do however require:
\(\displaystyle \tan^{-1}\left(\frac{W}{L} \right)\le\theta\le\frac{\pi}{2}\)
(2) If \(\displaystyle v_s=v_r\) then:
\(\displaystyle \theta=\cos^{-1}(1)=0\)
However, with $\theta=0$, the prisoner will not cross the river. So, what then is minimum ratio of \(\displaystyle \frac{v_s}{v_r}=k\) which causes the prisoner to swim straight for the safehouse, in other words, to swim the entire distance? We may set the distance BC to zero:
\(\displaystyle L-W\cot(\theta)=0\)
\(\displaystyle \cot(\theta)=\frac{L}{W}\)
\(\displaystyle \cot\left(\cos^{-1}\left(\frac{v_s}{v_r} \right) \right)=\frac{L}{W}\)
\(\displaystyle \frac{v_s}{\sqrt{v_r^2-v_s^2}}=\frac{L}{W}\)
\(\displaystyle \frac{kv_r}{\sqrt{v_r^2-(kv_r)^2}}=\frac{L}{W}\)
\(\displaystyle \frac{k}{\sqrt{1-k^2}}=\frac{L}{W}\)
\(\displaystyle k=\frac{L}{\sqrt{W^2+L^2}}\)
Thus if \(\displaystyle v_s\ge\frac{L}{\sqrt{W^2+L^2}}v_r\) then the prisoner should swim the entire way.
(3) As \(\displaystyle k\to 0\) then \(\displaystyle \theta\to\frac{\pi}{2}\).
Plugging in the data given to finish the problem, we have:
\(\displaystyle \theta=\cos^{-1}\left(\frac{6\text{ fps}}{12\text{ fps}} \right)=\cos^{-1}\left(\frac{1}{2} \right)=\frac{\pi}{3}=60^{\circ}\)
This is a valid angle as it satisfies:
\(\displaystyle \tan^{-1}\left(\frac{1}{5} \right)\le\theta\le\frac{\pi}{2}\)
Then another person made the observation:
I responded:
Interesting observation! Using this law we could state:
\(\displaystyle \frac{\sin(\theta_2)}{\sin(\theta_1)}=\frac{v_2}{v_1}\)
In this problem (the way I have it set up above), we have:
\(\displaystyle \theta_1=\frac{\pi}{2}\)
\(\displaystyle \theta_2=\frac{\pi}{2}-\theta\)
\(\displaystyle v_1=v_r\)
\(\displaystyle v_2=v_s\)
giving immediately:
\(\displaystyle \frac{\sin\left(\frac{\pi}{2}-\theta \right)}{\sin\left(\frac{\pi}{2} \right)}=\frac{v_s}{v_r}\)
\(\displaystyle \cos(\theta)=\frac{v_s}{v_r}\)
\(\displaystyle \theta=\cos^{-1}\left(\frac{v_s}{v_r} \right)\)
Let's generalize a bit to say we want to find the quickest path across two media:
https://www.physicsforums.com/attachments/2776._xfImport
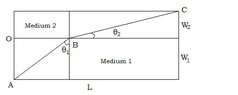
We are traveling from point A to point B then to point C by the quickest path possible. The question is, where should point B be placed?
I have set up $xy$ coordinate axes such that:
\(\displaystyle O=(0,0)\)
\(\displaystyle A=(0,-W_1)\)
\(\displaystyle B=(B,0)\)
\(\displaystyle C=(L,W_2)\)
The distance from A to B is:
\(\displaystyle AB=\sqrt{(B-0)^2+(0-(-W_1))^2}=\sqrt{B^2+W_1^2}\)
The distance from B to C is:
\(\displaystyle BC=\sqrt{(L-B)^2+(W_2-0)^2}=\sqrt{(L-B)^2+W_2^2}\)
The speed through medium 1 is $v_1$ and the speed through medium 2 is $v_2$. We assume both velocities are positive values. Thus, using the relationship between distance, constant velocity and time, we find the total time as a function of B is:
\(\displaystyle t(B)=\frac{\sqrt{B^2+W_1^2}}{v_1}+\frac{\sqrt{(L-B)^2+W_2^2}}{v_2}\)
Differentiating with respect to B, we find:
\(\displaystyle t'(B)=\frac{B}{v_1\sqrt{B^2+W_1^2}}+\frac{(B-L)}{v_2\sqrt{(L-B)^2+W_2^2}}=\frac{Bv_2\sqrt{(L-B)^2+W_2^2}+(B-L)v_1\sqrt{B^2+W_1^2}}{v_1v_2\sqrt{B^2+W_1^2}\sqrt{(L-B)^2+W_2^2}}\)
The denominator will always be positive, so we need only consider:
\(\displaystyle Bv_2\sqrt{(L-B)^2+W_2^2}+(B-L)v_1\sqrt{B^2+W_1^2}=0\)
\(\displaystyle Bv_2\sqrt{(L-B)^2+W_2^2}=(L-B)v_1\sqrt{B^2+W_1^2}\)
Let's take a moment to rewrite this:
\(\displaystyle \frac{B}{\sqrt{B^2+W_1^2}}\cdot\frac{\sqrt{(L-B)^2+W_2^2}}{L-B}=\frac{v_1}{v_2}\)
\(\displaystyle \frac{\frac{B}{\sqrt{B^2+W_1^2}}}{\frac{L-B}{\sqrt{(L-B)^2+W_2^2}}}=\frac{v_1}{v_2}\)
\(\displaystyle \frac{\sin(\theta_1)}{\sin(\theta_2)}=\frac{v_1}{v_2}\)
Thus, we have shown that Snell's law (or Descartes' law) is satisfied when \(\displaystyle t'(B)=0\).
Comments and questions should be posted here:
http://mathhelpboards.com/commentary-threads-53/commentary-using-snells-law-determine-fastest-escape-route-4204.html
This was my initial reply:
Let:
$L$ = distance upstream to the safehouse
$W$ = width of the river
$v_s$ = swimming speed
$v_r$ = running speed
All variables above are assumed to be positive.
I have set it up as follows:
https://www.physicsforums.com/attachments/2775._xfImport
The prisoner swims from A to B and runs from B to C. The distance from A to B is:
\(\displaystyle AB=W\csc(\theta)\)
The time this takes is:
\(\displaystyle t_s=\frac{W}{v_s}\csc(\theta)\)
The distance from B to C is:
\(\displaystyle BC=L-W\cot(\theta)\)
The time this takes is:
\(\displaystyle t_r=\frac{1}{v_r}(L-W\cot(\theta))\)
The total time then is:
\(\displaystyle t=t_s+t_r=\frac{W}{v_s}\csc(\theta)+\frac{1}{v_r}(L-W\cot(\theta))\)
\(\displaystyle \frac{dt}{d\theta}=-\frac{W}{v_s}\csc(\theta)\cot(\theta)+\frac{W}{v_r}\csc^2(\theta)=W\csc(\theta)\left(\frac{1}{v_r}\csc(\theta)-\frac{1}{v_s}\cot(\theta) \right)=0\)
Observing \(\displaystyle \csc(\theta)\ne0\) for all real $\theta$, we then use:
\(\displaystyle \frac{1}{v_r}\csc(\theta)-\frac{1}{v_s}\cot(\theta)=0\)
\(\displaystyle \csc(\theta)\left(\frac{1}{v_r}-\frac{1}{v_s}\cos(\theta) \right)=0\)
\(\displaystyle \frac{1}{v_r}-\frac{1}{v_s}\cos(\theta)=0\)
\(\displaystyle \cos(\theta)=\frac{v_s}{v_r}\)
\(\displaystyle \theta=\cos^{-1}\left(\frac{v_s}{v_r} \right)\)
This is why I used variables, so we can make a few observations:
(1) the angle is independent of $L$ and $W$. We do however require:
\(\displaystyle \tan^{-1}\left(\frac{W}{L} \right)\le\theta\le\frac{\pi}{2}\)
(2) If \(\displaystyle v_s=v_r\) then:
\(\displaystyle \theta=\cos^{-1}(1)=0\)
However, with $\theta=0$, the prisoner will not cross the river. So, what then is minimum ratio of \(\displaystyle \frac{v_s}{v_r}=k\) which causes the prisoner to swim straight for the safehouse, in other words, to swim the entire distance? We may set the distance BC to zero:
\(\displaystyle L-W\cot(\theta)=0\)
\(\displaystyle \cot(\theta)=\frac{L}{W}\)
\(\displaystyle \cot\left(\cos^{-1}\left(\frac{v_s}{v_r} \right) \right)=\frac{L}{W}\)
\(\displaystyle \frac{v_s}{\sqrt{v_r^2-v_s^2}}=\frac{L}{W}\)
\(\displaystyle \frac{kv_r}{\sqrt{v_r^2-(kv_r)^2}}=\frac{L}{W}\)
\(\displaystyle \frac{k}{\sqrt{1-k^2}}=\frac{L}{W}\)
\(\displaystyle k=\frac{L}{\sqrt{W^2+L^2}}\)
Thus if \(\displaystyle v_s\ge\frac{L}{\sqrt{W^2+L^2}}v_r\) then the prisoner should swim the entire way.
(3) As \(\displaystyle k\to 0\) then \(\displaystyle \theta\to\frac{\pi}{2}\).
Plugging in the data given to finish the problem, we have:
\(\displaystyle \theta=\cos^{-1}\left(\frac{6\text{ fps}}{12\text{ fps}} \right)=\cos^{-1}\left(\frac{1}{2} \right)=\frac{\pi}{3}=60^{\circ}\)
This is a valid angle as it satisfies:
\(\displaystyle \tan^{-1}\left(\frac{1}{5} \right)\le\theta\le\frac{\pi}{2}\)
Then another person made the observation:
I responded:
Interesting observation! Using this law we could state:
\(\displaystyle \frac{\sin(\theta_2)}{\sin(\theta_1)}=\frac{v_2}{v_1}\)
In this problem (the way I have it set up above), we have:
\(\displaystyle \theta_1=\frac{\pi}{2}\)
\(\displaystyle \theta_2=\frac{\pi}{2}-\theta\)
\(\displaystyle v_1=v_r\)
\(\displaystyle v_2=v_s\)
giving immediately:
\(\displaystyle \frac{\sin\left(\frac{\pi}{2}-\theta \right)}{\sin\left(\frac{\pi}{2} \right)}=\frac{v_s}{v_r}\)
\(\displaystyle \cos(\theta)=\frac{v_s}{v_r}\)
\(\displaystyle \theta=\cos^{-1}\left(\frac{v_s}{v_r} \right)\)
Let's generalize a bit to say we want to find the quickest path across two media:
https://www.physicsforums.com/attachments/2776._xfImport
We are traveling from point A to point B then to point C by the quickest path possible. The question is, where should point B be placed?
I have set up $xy$ coordinate axes such that:
\(\displaystyle O=(0,0)\)
\(\displaystyle A=(0,-W_1)\)
\(\displaystyle B=(B,0)\)
\(\displaystyle C=(L,W_2)\)
The distance from A to B is:
\(\displaystyle AB=\sqrt{(B-0)^2+(0-(-W_1))^2}=\sqrt{B^2+W_1^2}\)
The distance from B to C is:
\(\displaystyle BC=\sqrt{(L-B)^2+(W_2-0)^2}=\sqrt{(L-B)^2+W_2^2}\)
The speed through medium 1 is $v_1$ and the speed through medium 2 is $v_2$. We assume both velocities are positive values. Thus, using the relationship between distance, constant velocity and time, we find the total time as a function of B is:
\(\displaystyle t(B)=\frac{\sqrt{B^2+W_1^2}}{v_1}+\frac{\sqrt{(L-B)^2+W_2^2}}{v_2}\)
Differentiating with respect to B, we find:
\(\displaystyle t'(B)=\frac{B}{v_1\sqrt{B^2+W_1^2}}+\frac{(B-L)}{v_2\sqrt{(L-B)^2+W_2^2}}=\frac{Bv_2\sqrt{(L-B)^2+W_2^2}+(B-L)v_1\sqrt{B^2+W_1^2}}{v_1v_2\sqrt{B^2+W_1^2}\sqrt{(L-B)^2+W_2^2}}\)
The denominator will always be positive, so we need only consider:
\(\displaystyle Bv_2\sqrt{(L-B)^2+W_2^2}+(B-L)v_1\sqrt{B^2+W_1^2}=0\)
\(\displaystyle Bv_2\sqrt{(L-B)^2+W_2^2}=(L-B)v_1\sqrt{B^2+W_1^2}\)
Let's take a moment to rewrite this:
\(\displaystyle \frac{B}{\sqrt{B^2+W_1^2}}\cdot\frac{\sqrt{(L-B)^2+W_2^2}}{L-B}=\frac{v_1}{v_2}\)
\(\displaystyle \frac{\frac{B}{\sqrt{B^2+W_1^2}}}{\frac{L-B}{\sqrt{(L-B)^2+W_2^2}}}=\frac{v_1}{v_2}\)
\(\displaystyle \frac{\sin(\theta_1)}{\sin(\theta_2)}=\frac{v_1}{v_2}\)
Thus, we have shown that Snell's law (or Descartes' law) is satisfied when \(\displaystyle t'(B)=0\).
Comments and questions should be posted here:
http://mathhelpboards.com/commentary-threads-53/commentary-using-snells-law-determine-fastest-escape-route-4204.html
Attachments
Last edited: