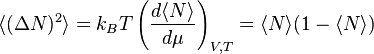\langle N \rangle is the Fermi-Dirac distribution, which is derived on that wikipedia page. So, you can perform the derivative yourself and verify the second equality.
The first equality can be derived as follows. First,
\displaystyle \langle ( \Delta N )^2 \rangle = \langle (N - \langle N \rangle )^2 \rangle = \langle N^2 - 2 \langle N \rangle N + \langle N \rangle^2 \rangle = \langle N^2 \rangle - \langle N \rangle^2.
Next, at constant volume and temperature, the grand-canonical partition function is given as the sum over all states, s of the Gibbs factors, e^{- (e_s - \mu n_s ) / k_B T} (check out the wikipedia page on partition function if this is unfamiliar):
\displaystyle Z = \sum_s e^{- (e_s - \mu n_s )/ k_B T}.
Here e_s and n_s are the state energy and occupation number. The Gibbs factor of a state measures the relative probability that that state is occupied. Hence, by definition,
\displaystyle \langle N \rangle = \frac{\sum_s n_s e^{-(e_s - \mu n_s)/k_B T}}{\sum_s e^{- (e_s - \mu n_s ) / k_B T}}.
Given these formulas for Z and \langle N \rangle, you should be able to show that
\displaystyle \langle N \rangle = k_B T \frac{1}{Z} \frac{dZ}{d \mu}.
I've taken it for granted that the derivatives are taken at constant volume and temperature.
Analogously, show that
\displaystyle \langle N^2 \rangle = (k_B T)^2 \frac{1}{Z} \frac{d^2 Z}{d \mu^2}.
Okay. At this point, I think you have all of the formulas you need to derive the first equality that you quoted from wikipedia. Just a little bit of ingenuity left. Good luck.