Variation of parameters to obtain PS of 2nd Order non-hom equation

[robot1000]

The question I'm trying to solve is:

y" - 6y' + 9y = \frac{exp(3x)}{(1+x)}

I formulated the Gen solution which are:

y1(x) = exp(3x) and y2(x) = xexp(3x)

I've then calculated the wronskian to get: exp(6x)

I then went onto to use the variation of parameters formula, which is where I got a bit stuck

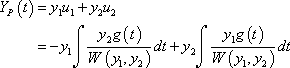
I ended up with

-exp(3x)*(x - ln(x+1) + xexp(3x)*ln(1+x)

The problem is, it just doesn't look right.

I would appreciate some guidance with this problem

 

[S_Happens]

Except for a parentheses that you missed to close the (x - ln(x+1)), it looks right to me. Why would you say that it doesn't look right, and what guidance do you expect to get?

 

[jackmell]

I would appreciate some guidance with this problem

Here's what you do. You solve it numerically first and then plot the analytic solution you get over the numeric solution. If they agree, right on top of one another, then there is very good odds your analytic solution is correct. If you're going to work with DEs, this is a very useful practice in my opinion. So learn how to set all this up in Mathematica or another CAS and you will never say again, "that don't look right."