Ellipses
- 17
- 0
Homework Statement
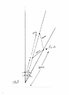
Amy wants to reach a destination that is 330m [E31 degrees N] from where she is. She travels a distance b towards [E20 degrees N] and then 100m to her destination. What is the distance b? (list all possible answers)
(Sorry I don't know how to get symbols)
Let [N] and [E] be positive.
delta d = 330m [E31 degrees N]
delta db = x [E20 degrees N]
delta dc = 100m [?]
Homework Equations
dx = d cos theta
dy = d sin theta
theta = tan^-1 (y / x)
The Attempt at a Solution
Well, first, I'm not allowed to use trig to solve (so no sine law for me). When I did it just to get the answer, I came up with x = 246 or x = 401.5 (approximate).
I've been trying this all of yesterday and I've got nothing. At this point I'm just randomly plugging things in and hoping something will come out.
I found the vector components of d, so
dx = +330cos31
dx = +282.87
dy = +330sin31
dy = +169.96
The rest of what I did is just kind of nonsense, now that I look at it. Anyone have any idea how to go about this? Any help would be appreciated! (And I know it probably isn't very clear so if any clarification is needed, just ask!)