Vectors and moments (Vector diagram, horizontal/vertical components, weight)

[jspake]

Hello,
I was solving a vector & moments question as a part of my revision and got stuck somewhere. I really need your help.. some sub-questions are solved, please correct me if I'm wrong.
Here's the question (Its kinda long) :

The free-body diagram shows three forces that act on a stone hanging at rest from two strings.

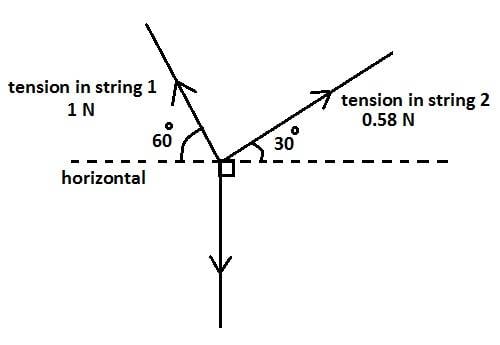
(a) Calculate the horizontal component of the tension in each string. Why should these two components be equal in magnitude?

String 1: =F cosθ = 1 x cos60 =0.5 N
String 2: =F cosθ = 0.58 x cos30 = 0.5 N

The components are equal in magnitude because the stone is at rest and there is no horizontal movement.

(b) Calculate the vertical component of the tension in each string

String 1: F Sin θ = 1 x sin60 = 0.87N
String 2: F Sinθ = 0.58 x sin30 = 0.29N

(c) Use your answer to (b) to calculate the weight of the stone

= 0.87 + 0.29 N
= 1.16N
(Not sure about this answer)

(d) Draw a vector diagram of the forces on the stone. This should be a triangle of forces

I don’t know how to solve this one – please help!

(e) Use your diagram in (d) to calculate the weight of the stone

This one too.. help!

 

[mfb]

The components are equal in magnitude because the stone is at rest and there is no horizontal movement.

No horizontal acceleration.

The approach for c is fine.

(d) Draw a vector diagram of the forces on the stone. This should be a triangle of forces

I don’t know how to solve this one – please help!

Hint: You already have all the forces in your diagram. Just shift the arrows around (and adjust their lengths) to get a triangle.
This will allow you to measure the length of the downwards force, too.