tensirk
- 12
- 0
Homework Statement
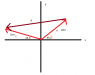
In the sum A+B = C, vector A has a magnitude of 10.0 m and is angled 46.5° counterclockwise from the +x direction, and vector C has a magnitude of 15.0 m and is angled 23.5° counterclockwise from the -x direction. What are the magnitude and the angle (relative to +x) of B?
________ m at _______ ° counterclockwise from the +x direction
Homework Equations
a2+b2=c2
The Attempt at a Solution
I have tried this:
A: (10cos(46.5))= 6.88; (10sin(46.25))= 7.25
C: (15cos(23.5))= 13.76; (15sin(23.5))= 5.98
Then:
13.76-6.88= 6.88
5.98-7.25=-1.27
After this I used the Pythagorean Theorem...
√(-1.27)2+(6.88)2 = 7m
However, this answer is incorrect.
From there I calculated tan-1(-1.27)/(6.88)= -10.46 degrees
Also obviously incorrect.
Help is greatly appreciated!