dapias09
- 28
- 0
Hello all,
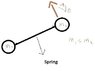
I'm confused with the center of mass concept. Regard the following problem, we have a spring with negligible mass joined to two masses m1 and m2 (m1=m2) on a table without friction force. At t=0 a thrust Vo (initial velocity) is given to m2 with direction perpendicular to the spring direction (see figure adjoint). How are the velocities at t=0 seen from the center of mass?
At t=0 the m1 velocity seen from the laboratory is zero but this particle isn't fixed on the table.
Well, I guess that I should calculate the velocity of the center of mass as:
Vcm = m1V1 + m2V2 / (m1 + m2) = m2V2 / (m1 +m2) = Vo / 2, since m1 and m2 are equals.
So the initial situation is equivalent to give a thrust to the center of mass with velocity Vo/2, but how I know what are the velocities of m1 and m2 seen of the center of mass?
Can anyone help me?
Thanks in advance.
I'm confused with the center of mass concept. Regard the following problem, we have a spring with negligible mass joined to two masses m1 and m2 (m1=m2) on a table without friction force. At t=0 a thrust Vo (initial velocity) is given to m2 with direction perpendicular to the spring direction (see figure adjoint). How are the velocities at t=0 seen from the center of mass?
At t=0 the m1 velocity seen from the laboratory is zero but this particle isn't fixed on the table.
Well, I guess that I should calculate the velocity of the center of mass as:
Vcm = m1V1 + m2V2 / (m1 + m2) = m2V2 / (m1 +m2) = Vo / 2, since m1 and m2 are equals.
So the initial situation is equivalent to give a thrust to the center of mass with velocity Vo/2, but how I know what are the velocities of m1 and m2 seen of the center of mass?
Can anyone help me?
Thanks in advance.