Velocity / Acceleration Diagrams of a Mechanism - Piston and a rotating rod

[Master1022]

Summary:: This is a question about finding the acceleration of a point in a mechanism

Hi,

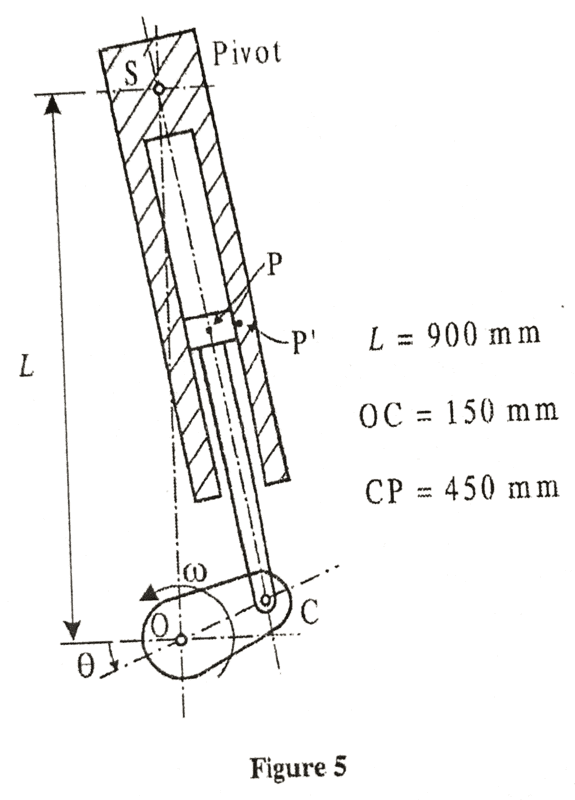
I have a question about the mechanism shown in the attached picture:

Question:
We are told that $\omega = 6 rad/s$ and the first part is asking me to find the acceleration of point P on the piston when $\theta = 90 degrees$.

My method:
One question I have is whether we can view this as a crank-slider mechanism? I usually see the mechanism depicted with a slider that is directly at C, but I am wondering whether this is what the question is getting at (especially for some of the later parts when acceleration diagrams are required)

Anyways, I have noted that when $\theta = 90 degrees$, that the lengths are: OC = 150 mm, CP = 450 mm, and SP = 300 mm.

I have first calculated $\vec v_c = \vec \omega_{OC} \times \vec r_{OC} = 6 \times (0.15) = 0.9 m/s$. Thus, in order to find the angular velocity of SP:
$$\vec v_c = \vec \omega_{SP} \times \vec r_{SC} = \vec \omega_{SP} \times 0.75 = 0.9 m/s$$ and thus $\vec \omega_{SP} = \frac{0.9}{0.75} = 1.2 rad/s$

To find the acceleration of point P on the piston, there are 4 possible components to consider: $\ddot r , - r \dot \theta ^ 2, r \ddot \theta,$ and $2 \dot r \dot \theta$. Am I correct in thinking that we only end up with the centripetal component $r \dot \theta ^ 2 = (1.2)^2 \times (0.3) = 0.432$ m/s^2 (pointing vertically upwards)

My reasoning is that:
At $\theta = 90$, the $\dot r = 0$ (of the sliding piston relative to the fixed point P) and thus the Coriolis component of the acceleration for bar CP will be 0. However, when drawing an acceleration diagram (not sure if this much working is required), it looks as if the angular acceleration of bar SP and CP are 0 such that the slider (piston) and rocker (fixed on rod) accelerations are vertically aligned (need to be vertically aligned because I believe that $\ddot r_{PP'} \neq 0$ and it will be vertical).

Any help is greatly appreciated.

Thanks

 

[mitochan]

The coordinate of P(Px,Py) is
$$P_x=OC \cos \theta -CP \sin \phi$$
$$P_y=OC \sin \theta + CP \cos \phi$$
where $\phi$ is angle OSC whose relation with others is
$$\frac{\sin \phi}{OC}=\frac{\cos (\phi-\theta)}{L}$$
or
$$\cos \phi=\frac{\frac{L}{OC}-\sin \theta}{\sqrt{cos^2\theta+(\frac{L}{OC}-\sin \theta)^2 }}$$ and
$$\sin \phi=\frac{cos\theta}{\sqrt{cos^2\theta+(\frac{L}{OC}-\sin \theta)^2}}$$
if I do not mistake.
Thus you get the formula of $P_y (\theta)=P_y (\omega t)$ and can derive its time derivatives.