- #1
MorgansRocks
- 6
- 1
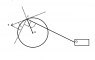
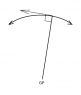
How do you calculate the Maximum Anglular Velocity (and angle at which this occurs) of a connecting rod which uses a slider-mechanism with an offset crank?
ω = 300 rpm, 10[itex]\pi[/itex] rad s-1
crank shaft, r = 50mm (0 → A)
connection rod, l = 200mm (A → B)
When crank angle = 45 degrees, the connection rod is horizontal and in-line with the piston.
I have calcualted, at 45 degrees, the velocity of the piston relative to 0 (1.11 m s-1) and the angular velocity of the con-rod, AB about A. (5.55 rad s-1 using a vector diagram for v, and ω=v/l
Not really looking, for an answer just a point in the right direction. Not came across a problem with an off-set crank before and don't really know where to start.
Thanks
ω = 300 rpm, 10[itex]\pi[/itex] rad s-1
crank shaft, r = 50mm (0 → A)
connection rod, l = 200mm (A → B)
When crank angle = 45 degrees, the connection rod is horizontal and in-line with the piston.
I have calcualted, at 45 degrees, the velocity of the piston relative to 0 (1.11 m s-1) and the angular velocity of the con-rod, AB about A. (5.55 rad s-1 using a vector diagram for v, and ω=v/l
Not really looking, for an answer just a point in the right direction. Not came across a problem with an off-set crank before and don't really know where to start.
Thanks