Govind_Balaji
- 83
- 0
Pl Help:Finding velocity using pythagorasTheorem and other velocities.
\left[
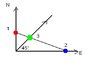
Three particles start moving simultaneously from a point on a horizontal smooth plane.
First particle moves with speed ##v_1## towards east, second particle moves towards north with speed ##v_2## and third one moves towards north east. The velocity of the third particle, so that three particles always lie on a straight line is,
https://fbcdn-sphotos-b-a.akamaihd.net/hphotos-ak-frc3/t1.0-9/10271500_1594365894121410_7484216690186519659_n.jpg
Let ##v_1=\frac{x_1}{t}##, ##v_2=\frac{x_2}{t}##, ##x_3=\frac{x_3}{t}##, where ##x_1, x_2, x_3## are displacement of three particles in ##t## seconds respectively.
##x_1=v_1t##
##x_2=v_2t##
##x_3=v_3t##
Displacement of third particle is the hypotenuse of the orange rectangle in the figure.
Displacement of particle A=2*adjacent side.
OB=Adjacent Side=##\frac{x_1}{2}##
Similarly, AB=Opposite side=##\frac{x_2}{2}##
##OA^2=x_3^2=\left[\frac{x_1}{2}\right]^2+\left[{\frac{x_2}{2}}\right]^2##
##x_3=\sqrt{\frac{x_1^2}{4}+\frac{x_2^2}{4}}##
##x_3=\frac{\sqrt{x_1^2+x_2^2}}{\sqrt{4}}##
##x_3=\frac{\sqrt{v_1^2t^2+v_2^2t^2}}{2}##
##x_3=\frac{\sqrt{(v_1^2+v_2^2)t^2}}{2}##
##x_3=\frac{t\sqrt{(v_1^2+v_2^2)}}{2}##
##v_3t=\frac{t\sqrt{(v_1^2+v_2^2)}}{2}##
##v_3=\frac{\sqrt{(v_1^2+v_2^2)}}{2}##
I checked my answer by substituting values for ##v_1## and ##v_2##. It's right.
I assume option D must be correct because it is the only answer which has the term 2.
I checked and D is the right answer but I should take
##v_3=\frac{\sqrt{(v_1^2+v_2^2)}}{2}##
to
##v3=\sqrt{2}\frac{v_1v_2}{v_1+v_2}##
\left[
Homework Statement
Three particles start moving simultaneously from a point on a horizontal smooth plane.
First particle moves with speed ##v_1## towards east, second particle moves towards north with speed ##v_2## and third one moves towards north east. The velocity of the third particle, so that three particles always lie on a straight line is,
- ##\frac{v_1+v_2}{2}##
- \sqrt{v_1v_2}s
- ##\frac{v_1v_2}{v_1+v_2}##
- ##\sqrt{2}\frac{v_1v_2}{v_1+v_2}##
Homework Equations
https://fbcdn-sphotos-b-a.akamaihd.net/hphotos-ak-frc3/t1.0-9/10271500_1594365894121410_7484216690186519659_n.jpg
The Attempt at a Solution
Let ##v_1=\frac{x_1}{t}##, ##v_2=\frac{x_2}{t}##, ##x_3=\frac{x_3}{t}##, where ##x_1, x_2, x_3## are displacement of three particles in ##t## seconds respectively.
##x_1=v_1t##
##x_2=v_2t##
##x_3=v_3t##
Displacement of third particle is the hypotenuse of the orange rectangle in the figure.
Displacement of particle A=2*adjacent side.
OB=Adjacent Side=##\frac{x_1}{2}##
Similarly, AB=Opposite side=##\frac{x_2}{2}##
##OA^2=x_3^2=\left[\frac{x_1}{2}\right]^2+\left[{\frac{x_2}{2}}\right]^2##
##x_3=\sqrt{\frac{x_1^2}{4}+\frac{x_2^2}{4}}##
##x_3=\frac{\sqrt{x_1^2+x_2^2}}{\sqrt{4}}##
##x_3=\frac{\sqrt{v_1^2t^2+v_2^2t^2}}{2}##
##x_3=\frac{\sqrt{(v_1^2+v_2^2)t^2}}{2}##
##x_3=\frac{t\sqrt{(v_1^2+v_2^2)}}{2}##
##v_3t=\frac{t\sqrt{(v_1^2+v_2^2)}}{2}##
##v_3=\frac{\sqrt{(v_1^2+v_2^2)}}{2}##
I checked my answer by substituting values for ##v_1## and ##v_2##. It's right.
I assume option D must be correct because it is the only answer which has the term 2.
I checked and D is the right answer but I should take
##v_3=\frac{\sqrt{(v_1^2+v_2^2)}}{2}##
to
##v3=\sqrt{2}\frac{v_1v_2}{v_1+v_2}##
Last edited: