Velocity of an Object given its position as a function of time

Click For Summary

Homework Help Overview

The discussion revolves around a problem related to determining the velocity of an object given its position as a function of time. Participants are exploring the relationship between position, speed, and acceleration in the context of calculus.

Discussion Character

  • Exploratory, Conceptual clarification, Mathematical reasoning

Approaches and Questions Raised

  • Participants discuss the correct interpretation of variables in the equations provided, particularly the distinction between position and speed. There are inquiries about using a calculator for quicker solutions and suggestions to utilize graphing tools for analysis.

Discussion Status

The discussion is ongoing, with some participants providing guidance on checking relevant equations and exploring the use of calculators. There is a mix of interpretations regarding the original poster's work and the feedback from their teacher.

Contextual Notes

There are mentions of potential misunderstandings regarding the equations used and the format of the submitted work, including issues with image orientation. The original poster's teacher indicated that a calculator could expedite the process, but the specifics of this suggestion remain unclear.

Strand9202
Messages
10
Reaction score
2
Homework Statement
Velocity of an object: Picture of problem and work attached
Relevant Equations
Speed =s(t)
Acceleration = s'(t)
Velocity = s"(t) or a'(t)
Attached is the problem and my work through the problem. I got the problem correct, but my teacher said this could be done quicker on a calculator. Any idea how it could be done quicker.

Screen Shot 2021-02-08 at 8.23.12 PM.png

Screen Shot 2021-02-08 at 8.23.25 PM.png
 

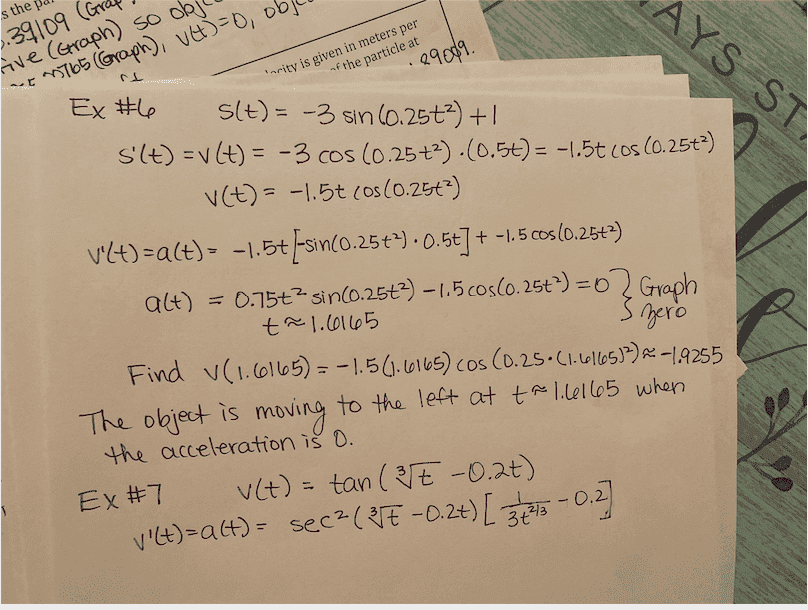
Attachments

  • 63452099186__DCDFFA52-49D9-4E49-B69A-84ED1CA44B81.jpeg
    63452099186__DCDFFA52-49D9-4E49-B69A-84ED1CA44B81.jpeg
    57.2 KB · Views: 167
  • 63452097838__A519283C-EC71-4527-BAEA-EDB73A167AA7.jpeg
    63452097838__A519283C-EC71-4527-BAEA-EDB73A167AA7.jpeg
    70.4 KB · Views: 152
Last edited:
Physics news on Phys.org
Check your relevant equations.
In #6, s(t) is the position, not the speed (an unfortunate choice of variables).
Speed is the derivative of position
Acceleration is the derivative of speed.
 
FactChecker said:
Check your relevant equations.
In #6, s(t) is the position, not the speed (an unfortunate choice of variables).
Speed is the derivative of position
Acceleration is the derivative of speed.
My work for number 6 is correct. My teacher checked it, but they said I could have used a calculator to find it quicker.
 
Sorry, I missed that your work was correct. In any case, I stopped reading when I saw that your "Relevant Equations" are all wrong.
Do you have a graphing calculator? Maybe your teacher means that you can look at the graph of position and determine the answer.
 
Strand9202 said:
I got the problem correct, but my teacher said this could be done quicker on a calculator.
Well, lots of things can be done more quickly on a calculator, but so what? If I were the teacher, and I've taught many calculus classes, I would be happy with your work.
As a PF member, I'm not quite as happy, since your images are all rotated by 90°. Your handwriting is very clear, though, and the images are well-lit.
 
Reply
  • Like
Likes   Reactions: berkeman
Mark44 said:
Well, lots of things can be done more quickly on a calculator, but so what? If I were the teacher, and I've taught many calculus classes, I would be happy with your work.
As a PF member, I'm not quite as happy, since your images are all rotated by 90°. Your handwriting is very clear, though, and the images are well-lit.
Sorry I thought I put the right side pictures up. I reedited and attached the correct ones.
 
Reply
  • Like
Likes   Reactions: berkeman

Similar threads

Proof that velocity of image by a plane mirror is negative of object
  • · Replies 5 ·
Replies
5
Views
2K
When is the velocity zero or changing?
  • · Replies 21 ·
Replies
21
Views
3K
Find nth derivative of e^m(arcsinx) where x=0
  • · Replies 7 ·
Replies
7
Views
3K
Can this function still be a constant function?
  • · Replies 11 ·
Replies
11
Views
2K
Finding the velocity of a rock thrown vertically on Mars
  • · Replies 6 ·
Replies
6
Views
1K
The first and second derivatives at various points on a drawn graph
  • · Replies 22 ·
Replies
22
Views
3K
Integration of acceleration in polar coordinates
  • · Replies 24 ·
Replies
24
Views
4K
Spirit evaporating from a bowl
  • · Replies 33 ·
2
Replies
33
Views
3K
Angular Velocity in the Rotating systems
  • · Replies 4 ·
Replies
4
Views
1K
Intermediate Value Theorem Problem on a String
  • · Replies 14 ·
Replies
14
Views
3K