Verification of ideal gas law experiment

[Voltux]

TL;DR Summary: I measured the mass of CO2. Can someone verify my calculations?

I took a soda bottle and filled it with Carbon Dioxide then weighted its mass as I changed pressures. My figures get very close (5-10%) within the calculated values for psig but not psi-absolute. Can someone confirm my results are correct? I think of this as confirmation bias but in a way I expected the values to be closer to the psia instead of psig.

Procedure
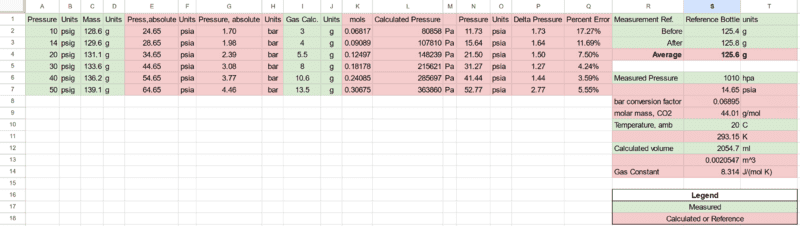
An empty "2L" bottle was filled with water to verify its actual volume. Approximately 2054g (mL) was measured on an 0.1g resolution electronic Ohaus balance.

From this the bottle was then emptied, weighted again after drying, then squeezed out of air followed by being filled with CO2 through a one-way valve. The bottle was then incrementally weighed followed by adjusting the pressure on the regulator and repeating the experiment for the values noted.

After the experiment values were placed in a spreadsheet, and calculated to adjust units along with measurements for ambient pressure and temperature were taken from similar electronic instruments.

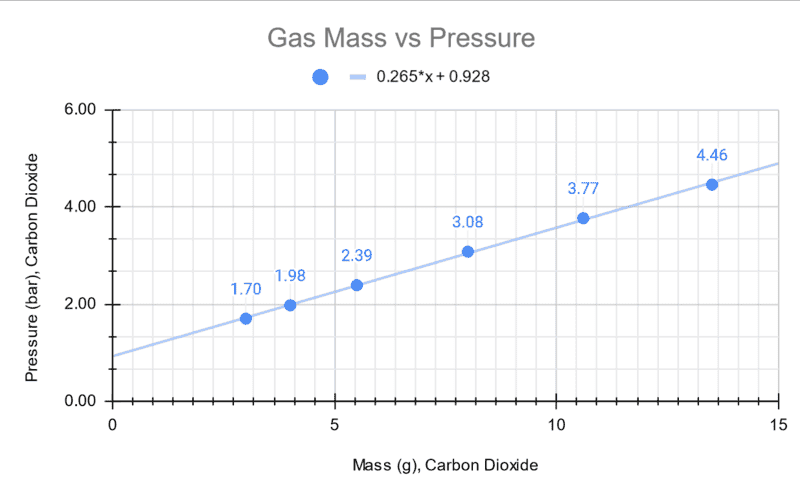
The experiment suggests that the relationship between pressure and mass are linear in nature over the range explored in this experiment. There is expected to be some error from the reference pressure point since it was obtained by an analog gas regulator gauge.

 

[hutchphd]

Was there air in the bottle or only CO2?? Does your legend make sense?

 

[Voltux]

Was there air in the bottle or only CO2?? Does your legend make sense?

The air in the bottle was removed by squeezing the bottle until essentially flat then placing a cap on the bottle that has a one way valve. The valve is a ball lock mechanism that is used to pressurize kegs. For the legend I just tried to highlight what were calculated values to help avoid confusion from the large amount of data.

• Pressure was read from the gas regulator
• Weight was from the electronic balance
• Atmospheric/room pressure was measured from an electronic barometer
• Temperature from a digital temperature sensor

Hope this helps. Any thoughts would be appreciated.

Thank you!

 

[Chestermiller]

Did you measure the temperature inside the bottle after it was filled? How long after filling the bottle did you weigh the bottle?

 

[hutchphd]

The pressure in the soda bottle before adding any CO2 is still 1 atm no matter how flat it is. It is not rigid under compression. So what do you expect the graph to do at zero?

 

[mjc123]

As I read it, when you weighed the "empty" bottle it was full of air. You then removed this air before adding CO₂. You need to correct your measured weights for the weight of this air.