- #1
- 5,844
- 550
Consider the Yukawa theory ##\mathcal{L}_0 = \bar{\psi}_0(i\not \partial - m_0 - g\phi_0)\psi_0 + \frac{1}{2}(\partial \phi_0)^2 - \frac{1}{2}M_0^2 \phi_0^2 - \frac{1}{4!}\lambda_0 \phi_0^4## with cutoff ##\Lambda_0##; a lower cutoff ##\Lambda < \Lambda_0## is then introduced with an effective theory ##\mathcal{L}_{\Lambda}##. We wish to then compute the 1-loop vertex corrections ##\tilde{c}_2, \tilde{c}_3## defined by ##\Pi(p^2) \approx \tilde{c}_3\Lambda^2 + \tilde{c}_2 p^2## in the diagrams below. The second diagram, with the scalar loop, is trivial to compute and isn't really the focus of my question so consider just the diagram with the fermion loop, which is of course the only diagram of the two that contributes to ##\tilde{c}_2##, this being the vertex correction of relevance.
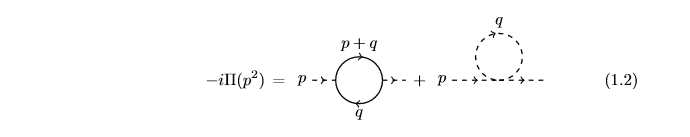
A straightforward calculation yields ##\tilde{c}_2 = \frac{g^2_0}{4\pi^2}\ln \frac{\Lambda_0}{\Lambda}##. The renormalized fine structure constant is defined by ##\alpha_{\Lambda} = \frac{g^2_{\Lambda}}{4\pi}## where the running coupling was calculated in class to be ##g_{\Lambda} = g_0(1 - c_1 - c_2 - \tilde{c}_2/2)## with the vertex corrections ##c_1 = \frac{g_0^2}{8\pi^2}\ln \frac{\Lambda_0}{\Lambda}, c_2 = \frac{g_0^2}{16\pi^2}\ln \frac{\Lambda_0}{\Lambda}## coming from other 1-loop diagrams that don't fall off as ##\frac{1}{\Lambda}## or faster (e.g. self-energy diagram).
Hence ##\alpha_{\Lambda} = \frac{g_0^2}{4\pi}(1 + \frac{5}{16\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0})^2##. Thus we find ##\Lambda \frac{d\alpha_{\Lambda}}{d\Lambda} = \frac{5}{8\pi^2}\frac{g_0^4}{4\pi}(1 + \frac{5}{16\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0})## and ##\alpha_{\Lambda}^2 = \frac{g_0^4}{16\pi^2}(1 + \frac{5}{16\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0})^4 \approx \frac{g_0^4}{16\pi^2}(1 + \frac{5}{4\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0}) + O(g_0^4) ##.
We have to show that ##\Lambda \frac{d\alpha_{\Lambda}}{d\Lambda} \propto \alpha_{\Lambda}^2## but I do not see how this is possible in the slightest given the above results, which I have verified time and time again by myself and with others. Does anyone know why the desired proportionality even holds? Thanks in advance!
A straightforward calculation yields ##\tilde{c}_2 = \frac{g^2_0}{4\pi^2}\ln \frac{\Lambda_0}{\Lambda}##. The renormalized fine structure constant is defined by ##\alpha_{\Lambda} = \frac{g^2_{\Lambda}}{4\pi}## where the running coupling was calculated in class to be ##g_{\Lambda} = g_0(1 - c_1 - c_2 - \tilde{c}_2/2)## with the vertex corrections ##c_1 = \frac{g_0^2}{8\pi^2}\ln \frac{\Lambda_0}{\Lambda}, c_2 = \frac{g_0^2}{16\pi^2}\ln \frac{\Lambda_0}{\Lambda}## coming from other 1-loop diagrams that don't fall off as ##\frac{1}{\Lambda}## or faster (e.g. self-energy diagram).
Hence ##\alpha_{\Lambda} = \frac{g_0^2}{4\pi}(1 + \frac{5}{16\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0})^2##. Thus we find ##\Lambda \frac{d\alpha_{\Lambda}}{d\Lambda} = \frac{5}{8\pi^2}\frac{g_0^4}{4\pi}(1 + \frac{5}{16\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0})## and ##\alpha_{\Lambda}^2 = \frac{g_0^4}{16\pi^2}(1 + \frac{5}{16\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0})^4 \approx \frac{g_0^4}{16\pi^2}(1 + \frac{5}{4\pi^2}g_0^2\ln \frac{\Lambda}{\Lambda_0}) + O(g_0^4) ##.
We have to show that ##\Lambda \frac{d\alpha_{\Lambda}}{d\Lambda} \propto \alpha_{\Lambda}^2## but I do not see how this is possible in the slightest given the above results, which I have verified time and time again by myself and with others. Does anyone know why the desired proportionality even holds? Thanks in advance!