- #1
lemonthree
- 51
- 0
Given that
\(\displaystyle
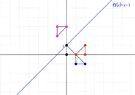
H_{1} \)= reflection about the line y = x + 1;
\(\displaystyle H_{2} \)= counterclockwise rotation of pi/2 about the point (1,0);
\(\displaystyle H_{3} \)= translation by 1 - i.
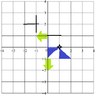
What is the image of the triangle and arrow under the map \(\displaystyle H = H_{1} *H_{2} * H_{3} \)?
I need help visualising the above transformation H. I know that \(\displaystyle H = H_{1} *H_{2} * H_{3} \), so we must perform the transformations from right to left (H3 first, then H2, and lastly H1). Now, in a question that provides the equation for \(\displaystyle H_{1},H_{2} , H_{3} \), I believe I can solve this by substituting the values into \(\displaystyle H_{1},H_{2} , H_{3} \) respectively. However, in this case, the question does not provide the equation and it is up to my visualisation.
I have attached photos showing my steps for each respectively. I have no trouble with translation (H3) as it is relatively easy to visualise.
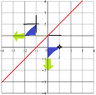
However, I struggle a little for the rotation about (1,0). I can't quite visualise "pivoting" the arrow and triangle about (1,0)...I would like to ask for some tips to aid in visualising such rotations better.
\(\displaystyle
H_{1} \)= reflection about the line y = x + 1;
\(\displaystyle H_{2} \)= counterclockwise rotation of pi/2 about the point (1,0);
\(\displaystyle H_{3} \)= translation by 1 - i.
What is the image of the triangle and arrow under the map \(\displaystyle H = H_{1} *H_{2} * H_{3} \)?
I need help visualising the above transformation H. I know that \(\displaystyle H = H_{1} *H_{2} * H_{3} \), so we must perform the transformations from right to left (H3 first, then H2, and lastly H1). Now, in a question that provides the equation for \(\displaystyle H_{1},H_{2} , H_{3} \), I believe I can solve this by substituting the values into \(\displaystyle H_{1},H_{2} , H_{3} \) respectively. However, in this case, the question does not provide the equation and it is up to my visualisation.
I have attached photos showing my steps for each respectively. I have no trouble with translation (H3) as it is relatively easy to visualise.
However, I struggle a little for the rotation about (1,0). I can't quite visualise "pivoting" the arrow and triangle about (1,0)...I would like to ask for some tips to aid in visualising such rotations better.