- #1
shakaflaka
- 6
- 0
Homework Statement
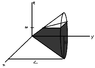
I need to find the volume of a cone covered with a plane z=h using multiple integrals. The scheme is something like this:
Homework Equations
Formula of the cone x^2-y^2-z^2=0
The Attempt at a Solution
I tried to integrate ∫∫∫(x^2-y^2-z^2)dxdydz in all different kinds of bounds, for example {x,0,L}, {y,-R,R}, {z,-R, H}, but the answer is always negative. I can't really get my head around the error, help please?
Attachments
Last edited by a moderator: