Water bell; got answer but shape's weird?

[unscientific]

Homework Statement

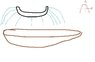
This question is about finding the smallest bowl to contain all the water being spurt out of a water spray head.


They used the lagrange multipliers to solve it which I understand, but the the envelope doesn't look like a parabola to me??

Isn't the envelope supposed to be a curve that is parallel to a certain point on every member of a family curve?

The Attempt at a Solution

I don't even see how it's possible to draw a curve that's tangential to all water-jet curves..

 

[voko]

They did not use Lagrange multipliers. An envelope of a family of curves F(x, y, p) = 0, where p is parameter, is obtained by \frac {\partial F} {\partial p} = 0, which is what they do.

 

[HallsofIvy]

Your picture is very strange. You seem to have water coming from a head that is convex downward and raised above the surface of the water. The situation described in the post has a hemispherical (convex upward) head at the level of the surface of the water.

 

[unscientific]

Your picture is very strange. You seem to have water coming from a head that is convex downward and raised above the surface of the water. The situation described in the post has a hemispherical (convex upward) head at the level of the surface of the water.

LOL i thought it was the bottom hemisphere. That was the first picture that came to my mind when i thought of a tap and a basin (come on, who builts a tap that spurts upwars? :P)


I finally see it, thank you!


I seem to lack the imagination.

 

[Ray Vickson]

LOL i thought it was the bottom hemisphere. That was the first picture that came to my mind when i thought of a tap and a basin (come on, who builts a tap that spurts upwars? :P)


I finally see it, thank you!


I seem to lack the imagination.

Well, who builds a water feature with a spray head at water level, pointing down?

RGV

 

[HallsofIvy]

Think of it not as a "tap" but as a fountain in an outdoor pool.

(But they are making some very peculiar bathroom fixtures now. I recently had my bathroom remodeled. I looked at some bathroom sinks that are acryic hemispheres sitting on top the counter. I stared at them for a while, shook my head, and walked on.)