gloo
- 261
- 2
In the picture i have included I was wondering if the same downward force (black arrows) applied in the diagrams would result in an increased pressure as the water comes up through the same size hole.
I am assuming that both Diagram B and C will result in a higher pressure because of the narrow or funnel shape because more water is forced at a time through the hole with the same given force? If not can someone explain why?
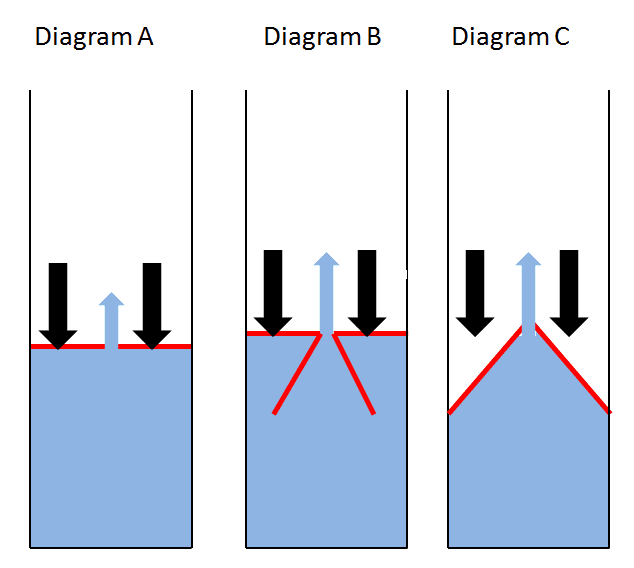
I am assuming that both Diagram B and C will result in a higher pressure because of the narrow or funnel shape because more water is forced at a time through the hole with the same given force? If not can someone explain why?