Wave Optics & Two-Slit Interference Explanation

[hdp12]

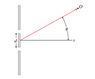
I have an online homework question and my classmate told me the answer but I would really like someone to explain to me how that answer was determined. I do not understand. Q: Consider the electric field observed at a point O that is far from the two slits, say at a distance r from the midpoint of the segment connecting the slits, at an angle θ from the x axis. Here, far means that r≫d, a regime sometimes called Fraunhofer diffraction.

The critical point is that the distances from the slits to point O are not equal; hence the waves will be out of phase due to the longer distance traveled by the wave from one slit relative to the other. Calculate the phase Φ_lower(O,t) of the wave from the lower slit that arrives at point O.

EQUATIONS:
E(x,t)=E_leftcos[2π/λ(x−ct)].
Φ(x,t)=kx−ωt
ω=2πf
k=2π/λ

SOLUTION:
Φ_lower(O, t) = 2π/λ (r−ct) + π/λ dsin(θ)

I just really don't understand how that is derived...
can someone please help explain?

 

[Simon Bridge]

That's the trouble with just having someone tell you the answer, you end up not understanding it.
The reason it was given you as an exercise is that you benefit best from working it out yourself.
Start like this:

What determines the phase of the wave?

 

[hdp12]

That's the trouble with just having someone tell you the answer, you end up not understanding it.
The reason it was given you as an exercise is that you benefit best from working it out yourself.

I understand that, and I rarely ask others for the solution. However I had to turn in the assignment so I got the answer but am currently going back and redoing it so as to understand it myself. I want to know how to do the problem. I promise I am neither a cheater nor a slacker. I actually enjoy a majority of the problems we are given, this one just tripped me up.

You ask what determines the phase of the wave?
Isn't it derived using the wavenumber or wavelength, distance, angular frequency or frequency, and time? such as in the formula Φ(x,t)=kx−ωt

 

[Simon Bridge]

The phase is a physical characteristic of the shape of the wave.
It is better to think first of the physics or the geometry and then worry about equations.

In terms of the phasor model - the phase is the angle the phasor makes to the real axis.
In terms of the traditional sine wave, points of equal phase have the same instantaneous amplitude and slope.
The equation comes out as $\Phi(\vec r, t) = \vec k\cdot\vec r -\omega t + \delta$.

If you pick the origin for time where $\Phi(0,0)=0$, then, for a spherical wave, what is $\Phi(r,0)$ for some distance $r$ from the origin.

Then keep going - I cannot really be much help if I don't see where you get derailed.
If you are having trouble understahding how the above helps - don't worry: just show me your best attempt.

 

[HalfLostAndSearching]

Sure! Let's break down the solution step by step to understand how it was derived.

First, we need to understand the concept of phase in wave optics. Phase refers to the position of a wave in its cycle at a given point in space and time. It is typically measured in radians and can be thought of as the angle of the wave at a specific point.

Next, we need to understand the equations given in the problem. The first equation, E(x,t) = Eleftcos[2π/λ(x−ct)], represents the electric field at a point x and time t, where Eleft is the amplitude of the wave, λ is the wavelength, and c is the speed of light. This equation is known as the wave equation and describes the behavior of a wave in space and time.

The second equation, Φ(x,t) = kx−ωt, represents the phase of the wave at a point x and time t, where k is the wave number (2π/λ) and ω is the angular frequency (2πf).

Now, let's look at the problem at hand. We are trying to calculate the phase Φlower(O,t) of the wave from the lower slit that arrives at point O. To do this, we need to consider the distance traveled by the wave from the lower slit to point O. In this case, the distance is r, as stated in the problem.

However, we also need to take into account the fact that the distances from the slits to point O are not equal. This means that the waves from each slit will have traveled different distances and therefore will have different phases when they reach point O. This is what causes the interference pattern we observe in the two-slit experiment.

To calculate the phase Φlower(O,t), we need to add the phase due to the distance traveled (2π/λ (r−ct)) to the phase due to the angle of arrival (π/λ dsin(θ)). The angle of arrival is given by the equation dsin(θ), where d is the distance between the two slits and θ is the angle at which the wave arrives at point O.

Combining these two phases, we get the solution Φlower(O,t) = 2π/λ (r−ct) + π/λ dsin(θ). This equation takes into account the different distances and angles of arrival for the wave from the lower