Waveform produced by a collapsing magnetic field

[etotheipi]

Wow

To try to begin to understand your method I drew a picture, I wondered if it agrees with what you had in mind (or whether it's completely off )? The red line is the worldline of the charge, and at $t' = 0$, its 4-velocity is parallel to the $t'$ axis, so the charge is instantaneously at rest at this time in $S'$. Also, the vector $R$ joining this event to $E$ is null, and thus parallel to the yellow lightcones.

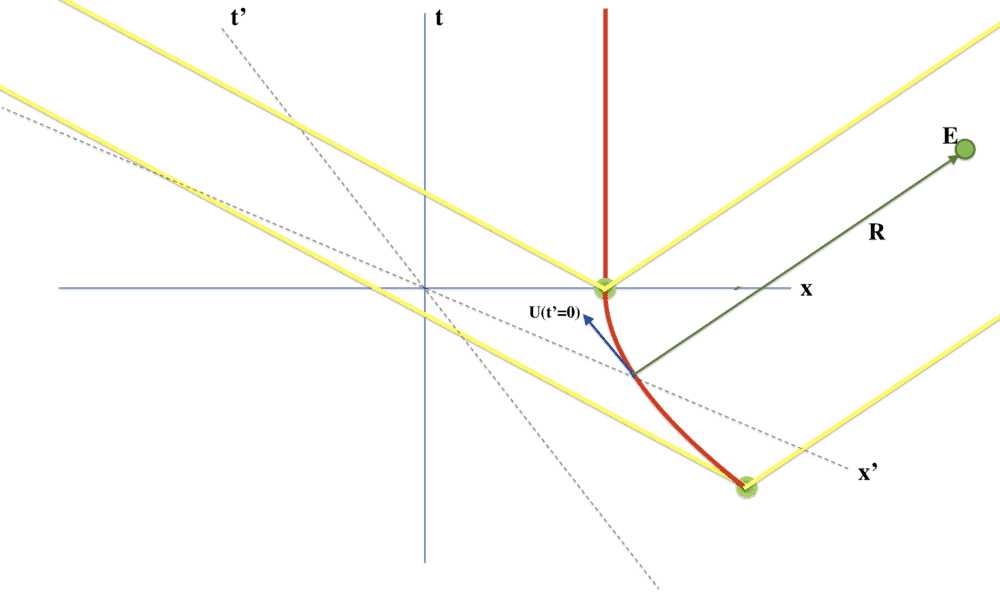
How does that look?

 

[Ibix]

That's it. Thanks - I was planning to draw a Minkowski diagram myself, but got side-tracked with the simplification stuff.

Looking at that, I wonder if I've got the wrong sign on my solution for $v$, since it should be negative. I'll have a look tomorrow.

 

[vanhees71]

Constant proper acceleration is also among the more complicated examples. Even Pauli got it wrong (not so Sommerfeld, but this has been overlooked for some time). I think the resolution of the paradox that apparently there seems to be no radiation is given by Griffiths in

https://arxiv.org/abs/1405.7729
https://aapt.scitation.org/doi/10.1119/1.4875195
https://doi.org/10.1119/1.4906577 (Erratum)

Also in this case there are singular contributions to the fields, because the speed of the particle goes asymptotically to $c$, and these conributions solve the problem.