Wavelength and destructive interference

In summary, the two speakers in the figure are producing identical sound waves with solid lines representing constructive interference regions and dashed lines representing destructive interference regions. Point 1 is located 662.15 m from the bottom speaker and 742.9 m from the top speaker. The problem is asking for the wavelength of the sound waves, which can be found using the equation v = f*lambda, where v is the speed of sound (assumed to be 343 m/s) and lambda is the wavelength. To solve for lambda, the Pythagorean theorem can be used to find the distance between the two speakers, but this method did not work. A picture is provided for reference.
  • #1
boogiepicker
3
0

Homework Statement



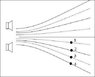
In the figure the two speakers are producing identical sound
waves. The solid lines represent constructive interference regions and the dashed lines represent destructive interference regions. The point labeled 1 is 662.15 m from the bottom speaker
and 742.9 m from the top speaker.

What is the wavelength of the sound waves


Homework Equations


v = f*lambda?, assuming v = 343 m/s
Pythagorean I believe has to be used but I'm not sure


The Attempt at a Solution


Attempted Pyth. to find distance between speakers, thinking this would be the PLD and then I'd be able to find the wavelength from there. This did not work.

Here's a picture:
 
Physics news on Phys.org
  • #2
only way I could get correct image on here is via attachment
 

Attachments

  • phys dang.jpg
    phys dang.jpg
    14.1 KB · Views: 389

FAQ: Wavelength and destructive interference

1. What is a wavelength?

A wavelength is a physical property of a wave that represents the distance between two adjacent points on the wave that are in phase, or have the same position and direction of oscillation.

2. How is wavelength measured?

Wavelength is typically measured in meters (m) or nanometers (nm). It can be measured by taking the distance between two consecutive peaks or troughs of a wave.

3. What is destructive interference?

Destructive interference is a phenomenon that occurs when two waves with opposite amplitudes and identical wavelengths meet and cancel each other out, resulting in a decrease in the overall amplitude of the resulting wave.

4. How does destructive interference affect the overall intensity of a wave?

Destructive interference can significantly decrease the overall intensity of a wave, as the amplitudes of the two interfering waves cancel each other out. The more in-phase the two waves are, the greater the decrease in intensity will be.

5. How is destructive interference used in applications?

Destructive interference can be used in various applications such as noise-cancellation technology, where two sound waves with opposite amplitudes are used to cancel each other out and reduce overall noise. It is also used in optics to create dark zones in diffraction patterns.

Similar threads

Olympiad question on destructive interference
Replies
3
Views
943
Destructive vs Constructive interference
Replies
2
Views
3K
What is the Maximum Wavelength for Constructive Interference of Sound Waves?
Replies
3
Views
2K
Sound Wave Interference and Finding the Path Differences with Diagrams
Replies
20
Views
3K
Is there constructive or destructive interference?
Replies
20
Views
2K
Can you please check this (destructive interference).
Replies
8
Views
1K
Destructive interference and constructive interference
Replies
4
Views
2K
Frequency at which no destructive interference occurs
Replies
7
Views
2K
HW Question regarding double-slit interference
Replies
8
Views
2K
Difference in Wave Phase Question
Replies
8
Views
3K

Hot Threads

Recent Insights

Back
Top