Wavelength and destructive interference

AI Thread Summary
The discussion revolves around calculating the wavelength of sound waves produced by two speakers, with specific distances provided for a point of interest. The speakers create regions of constructive and destructive interference, and the user is attempting to apply the Pythagorean theorem to find the path length difference (PLD) between the speakers. The velocity of sound is assumed to be 343 m/s, and the relationship v = f*lambda is referenced for calculating the wavelength. The user's initial approach using the Pythagorean theorem did not yield the expected results. Clarification on the correct method to determine the wavelength is sought.
boogiepicker
Messages
3
Reaction score
0

Homework Statement



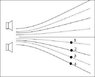
In the figure the two speakers are producing identical sound
waves. The solid lines represent constructive interference regions and the dashed lines represent destructive interference regions. The point labeled 1 is 662.15 m from the bottom speaker
and 742.9 m from the top speaker.

What is the wavelength of the sound waves


Homework Equations


v = f*lambda?, assuming v = 343 m/s
Pythagorean I believe has to be used but I'm not sure


The Attempt at a Solution


Attempted Pyth. to find distance between speakers, thinking this would be the PLD and then I'd be able to find the wavelength from there. This did not work.

Here's a picture:
 
Physics news on Phys.org
only way I could get correct image on here is via attachment
 

Attachments

  • phys dang.jpg
    phys dang.jpg
    14.1 KB · Views: 429

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Olympiad question on destructive interference
Replies
3
Views
1K
Destructive vs Constructive interference
Replies
2
Views
4K
What is the Maximum Wavelength for Constructive Interference of Sound Waves?
Replies
3
Views
3K
Sound Wave Interference and Finding the Path Differences with Diagrams
Replies
20
Views
5K
Is there constructive or destructive interference?
Replies
20
Views
3K
Can you please check this (destructive interference).
Replies
8
Views
2K
Destructive interference and constructive interference
Replies
3
Views
3K
Frequency at which no destructive interference occurs
Replies
7
Views
2K
HW Question regarding double-slit interference
Replies
8
Views
2K
Difference in Wave Phase Question
Replies
8
Views
3K

Hot Threads

Recent Insights

Back
Top