Webpage title: Calculating Centripetal Force in a Sliding Mass Problem

[pulau_tiga]

I am having troubles with this physics question, I'm not really sure on how to set it up and everything.

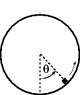
question: A mass M of 3.60×10-1 kg slides inside a hoop of radius R=1.20 m with negligible friction. When M is at the top, it has a speed of 5.33 m/s. Calculate size of the force with which the M pushes on the hoop when M is at an angle of 36.0 degrees.
(see attachment).

my answer:
Centripetal a = v^2/r = (5.33 m/s)^2 / 1.20 m = 23.7 m/s^2

Normal force = y component of gravity (if we take y-axis to be perpedicular to the tangent of the hoop at that point).

= mgcos(36.0) = (3.60×10-1 kg)(9.81 N/kg)(cos36.0)
=2.86 N

If anyone could help me, I'm not sure what I'm suppose to do. 2.86 N is not the answer, I know. But I'm so confused. Thanks.

 

[maverick280857]

Do you know that

\sum F_{n} = \frac{mv^2}{r}

In words, the net normal force (directed towards the center) provides the necessary centripetal force for circular motion.

Cheers
Vivek

 

[maverick280857]

You have taken one step in the right direction. If you resolve the weight along two (mutually perpendicular) axes, you will see that the resultant of the normal reaction (which by the way is directed towards the center at ALL times since the mass slides inside the hoop) and the component of weight along the normal provides the centripetal force. You know v at the highest point, you can calculate v as a function of theta (using energy considerations) and plug it in here.

Your mistake is that you have forgotten to take the centripetal acceleration into consideration. There is after all circular motion here and so to it, we must attribute a centripetal force...which gives

N = mg\cos\theta + \frac{m(v(\theta))^2}{r}

whereas you have written merely

N = mg\cos\theta

Do you see the difference? You have indeed computed the missing term but have not used it anywhere.

Your second mistake is to assume that the speed at the top is the same as the speed at the bottom. Please note that in a vertical plane, the speed will change and will be a function of the angle theta. Intuitively you see no reason for speed to remain constant--just as a ball projected in the air has nonconstant speed being accelerated and decelerated at different times, a ball moving in a circle in a vertical plane will be subject to the constant acceleration g acting vertically downwards at all times.

Actually circular motion is a special case of curvilinear motion where r = constant. A more advanced analysis of curvilinear motion in polar coordinates yields a more general expression which reduces to the one for circular motion in the case r = constant (and for uniform circular motion when the angular velocity is constant as well).

Hope that helps...

Cheers
Vivek

PS--Start by finding v as a function of theta. Remember that in the convention chosen for theta, you know v at theta = 180 degrees.

 

[WillP]

I have to do the EXACT same problem (well, with different numbers)

it's due in a couple of hours and I can't figure it out either! I've tried Fnet = mv^2 / R but it doesn't help...

can you guys explain how to find V at the angle a little more? I think if I could find the correct velocity at the point it would be easier.
my problem is:

"A mass M of 7.00×10-1 kg slides inside a hoop of radius R=1.40 m with negligible friction. When M is at the top, it has a speed of 5.75 m/s. Calculate size of the force with which the M pushes on the hoop when M is at an angle of 43.0 degrees."

the hint they give is:
"Hint: If you know the radius of the hoop and the angle, you can calculate how far the mass is below the level of the hoop centre, and thus how far below the top of the hoop, when in the position shown. Since you know the speed at the top of the hoop, you can use conservation of mechanical energy to find its speed, and thus its centripetal acceleration, at the position shown. You then need to draw the free body diagram for the mass. Remember that there are two forces acting on the mass; gravity and the normal force exerted by the hoop (which is what you are asked to find). "

but it's a little confusing to me... I still have 5 tries left for the right answer. Help please.

my workings:

Etop = mv^2 + mgh
= 1/2)(.7)(5.75)^2 + .7(9.8)(2.8)
= 30.78 J
I figured h would = 2.8 cause it's the the radius doubled giving the max height... maybe that's where I'm gone wrong.
anyway:

Etop = E43degrees
30.78 = .5(.7)(v^2) + .7(.955)(9.8)
v = 8.32m/s

Fnet = mv^2/R
mg - Fn = mv^2/R
Fn = mv^2/r - mgcos43
Fn = .7(8.32)^2/1.4 - .7(9.8)cos43
Fn= 29.59 N which is wrong.

I found the h=.955 with 1.4sin43 I think the reason I'm getting this problem wrong is in finding the heights

the graphic given was even the same (author:don't suppose you attend Memorial University of Newfoundland do you?)

 

[CartoonKid]

I think your Fnet should be Fn-mg.

 

[Gokul43201]

I have to do the EXACT same problem (well, with different numbers)

I found the h=.955 with 1.4sin43 I think the reason I'm getting this problem wrong is in finding the heights

This is exactly where the mistake is. The rest of the working is perfectly correct. (except, once you make this change you'll see that cartoonkid's correction will give you the right sign)

h(top) = 2R = 1.4*2 = 2.8m (that's fine)
h(43 deg) = R - Rcos43 = R(1-cos43), assuming that the angle of 43 deg is measured from the downward vertical, as shown in the attached picture of pulau's post.

Make sure you understand why this is the correct way to calculate the height.

This one change should fix it.

Pulau, read WillP's post, with the one correction that I've suggested (and cartoonkid's catch).

 

[WillP]

Yes, that worked perfect. I -think- I understand why that's the height... just having a hard time visualizing it.
thanks a lot guys.