Weight required to balance a boom stand?

[xseven]

Hi!

I am trying to build a stand with a boom arm for my acting classes and I need to find the weight required to balance it. The problem is that it looks like I was more like a swan when I was swimming in the physics lessons ... no a lot of drops stayed on my plumage ... :)
Help?!

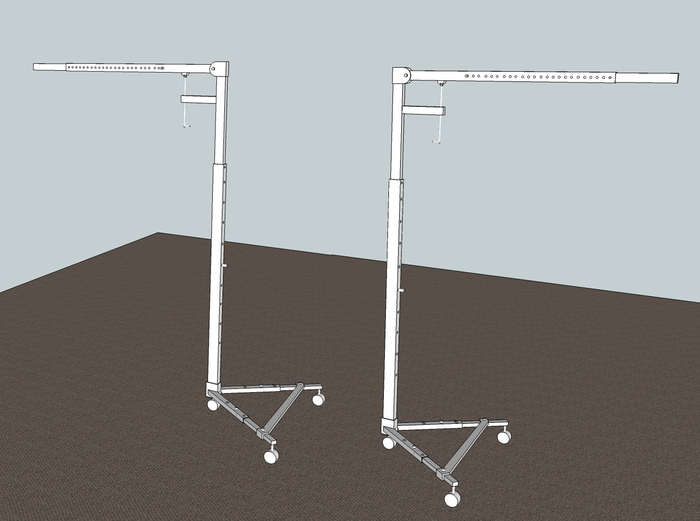
Data:

Stand height: "H" (more or less 2 m fully extended)
Boom arm: "B" (again, more or less 2 m fully extended) - the arm can be lifted rotating a threaded rod so I assume the length of the boom is (for the purpose of a formula) a+b (where "a" will be between the hinge and the rod's point of contact)
Legs: "L"

The questions that are troubling me are as follows:

1. What is the most stable configuration of legs? an angle of 90°? 60°?
2. What formula can calculate the weight required to stabilize the system when weight "W" (more or less 10 KG) is attached to the boom arm fully extended pointing away from the legs?
3. What formula can calculate the weight required to stabilize the system when weight "W" is attached to the boom arm fully extended pointing in the same direction with the legs?
... And 4 (already feeling that I push the limits of your patience) ... I would like the threaded rod to be as short and as close as possible to the main pole - is there a way to calculate the force required to raise the boom arm with the weight to a 45° angle from the horizontal position? How close to the stand can I put it and still manage to have a smooth rotating action?

Humbly yours,

Cat

 

[zoobyshoe]

#2 is the easiest to answer. Measure the length of the arm with the boom fully extended. Then measure the distance from the apex of the leg triangle (where it meets the upright) to the point where the counterweight will be placed on the legs. This will give you a ratio of length to length. Let's say it's 1.02 meters to .43 meters. The weights that will balance will be to each other in the inverse ratio to this ratio of lengths. The weight of 10 kg is a given. You have to find that weight which is to 10 kg as 1.02 meters is to .43 meters. That means solve for: ?/10 = 1.02/.43 The product of the means equals the product of the extremes, so multiplying means gives 10 X 1.02 = 10.2. To find the missing extreme 10.2 is divided by .43 = 23.72 kg counterweight needed.

That's not the weight you should use, though. That weight will only just balance. The thing could still be knocked over with a feather unless you add much more ballast. The calculation just gets you the absolute minimum counter weight that will prevent it from falling over by itself.

 

[xseven]

So ... assuming that the boom arm will be 2m and the distance from the apex to the counterweight will be 0.5 m that will give a ratio of 4:1 - for 10KG on the boom arm a 40KG weight will act as a balance ballast. (ignoring the weight of the boom arm itself etc)
What would be the approach for #3?

Thank you for your help!

 

[zoobyshoe]

So ... assuming that the boom arm will be 2m and the distance from the apex to the counterweight will be 0.5 m that will give a ratio of 4:1 - for 10KG on the boom arm a 40KG weight will act as a balance ballast. (ignoring the weight of the boom arm itself etc)
Thank you for your help!

You're welcome. Looks like you have it down.

What would be the approach for #3?

I'm not so sure about this one, but I think the procedure would be to subtract the leg distance (.5 m) from the boom length (2m) for a new ratio of 1.5 to .5. The counterweight, 30 kg, would have to be placed as close up to the upright as possible.

Here, again, this is the absolute minimum weight to prevent the thing from falling over by itself. In practice you should add much more. Just have to experiment, adding weight till you can knock it and bump into it a reasonable and realistic amount.

If this is to hold a camera I would redesign it altogether to have three long legs set at 120 degrees. I would make the boom like a mike boom, sticking out in both directions with a movable counterweight on it. In that way you could keep the center of gravity of the boom, camera, and counter weight pretty much over the upright. I would mount the boom to the upright with a large bolt and wing nut (with washers). It could be pivoted up and down by loosening and tightening the wing nut.

 

[PJC01]

Hi Cat,

It sounds like you have a complex project on your hands! I can definitely provide some guidance and formulas to help you determine the weight required to balance your boom stand.

To begin, let's address your first question about the most stable configuration of legs. The stability of a stand depends on the center of mass and the base of support. A wider base of support will provide more stability, so an angle of 90° between the legs would be more stable than 60°. However, for practical purposes, a 60° angle may be sufficient and also allow for more compact storage of the stand.

Next, we can move on to calculating the weight required to stabilize the system when a weight "W" is attached to the boom arm fully extended. To determine this, we need to consider the forces acting on the stand. The weight of the stand itself, the weight of the weight "W", and the weight of the counterweight needed to balance the system. We can use the principle of moments to calculate the weight of the counterweight needed. The formula is W1 x D1 = W2 x D2, where W1 is the weight of the weight "W", D1 is the distance of W1 from the fulcrum (the hinge in this case), W2 is the weight of the counterweight, and D2 is the distance of W2 from the fulcrum. We can rearrange this formula to solve for W2, which will give us the weight of the counterweight needed to balance the system.

For your third question, the formula will be the same as above, except D1 will be the distance from the fulcrum to the point where the weight "W" is attached. Again, we can rearrange the formula to solve for W2, which will give us the weight of the counterweight needed in this scenario.

Finally, for your last question about calculating the force required to raise the boom arm to a 45° angle, we need to consider the torque required. Torque is the force applied multiplied by the distance from the point of rotation. In this case, the force will be the weight of the weight "W" and the distance will be the distance from the fulcrum to the point where the weight "W" is attached. To determine how close the threaded rod can be to the main pole, you will need to experiment with different distances and see how